Performance Curve
Amdahl’s Law
The execution time of a system, in general, has two fractions – a fraction fenh that can be speeded up by factor n (taking the advantage of n processor), and the remaining fraction 1 - fenh that cannot be improved. Thus, the possible speedup is:
Speedup = Old time / New time
1
= ──────────
1 – fenh + fenh/n
So assigning a job to multi-processor compute node does not reduce your program computation time necessarily. It depends on your coding style as well, that is how you have parallelised your code.
Even if you fully parallelize your code, the maximum possible speed up is: 1/(1-fenh) when n-->∞ which means there must be some part of your code which is sequential.
For Parallel Processors with Distributed Memory network architecture is like:
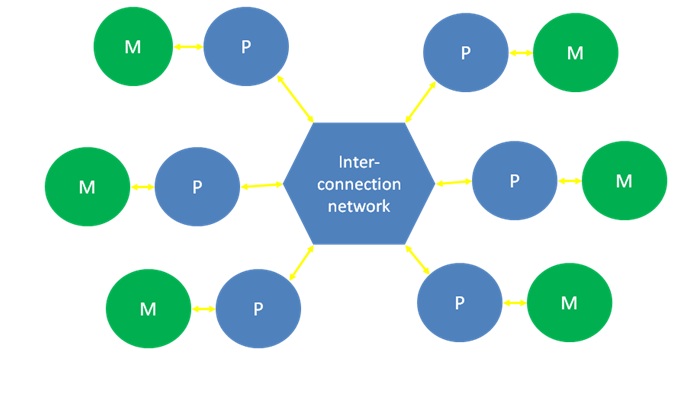
Each processor has it’s own memory. To make the data consistent, data written by any of these processor needs to be updated through out all of the memory. So there is a communication over head β(N-1).
β is the time it requires to update memory – communication factor
For N=1 processor, Communication o/h = β(1-1) = 0
We have 40Gb/s switch for intra-node communication in between 16 blades and 10Gb/s switch for inter-node communication. Each blade has 2 cpu, quad-core each, 8 processor as total. So as long as a job was assigned to max 8 proc, there may be no inter-blade (intra-node) communication o/h but it might have taken 8 proc from different blades and incurred some inter-blade comm. o/h!
Communication O/H variability:
- β(N-1) increases with increasing number of processor
- If the program computation time is large (say 3-4 days) then asking for so many processor is ok and you’ll get increased performance—In that case β(N-1) is negligible say 20 minutes
- If program computation time is small (say 2 min) and you asked for so many processor that will incur extra communication over head (say 20 minutes,) then it will take 2+20min =22 min instead of 2 minute and thus reduces the performance
- There is always an optimum no. of processor for any particular program at any certain time – certain time implies β can increase if someone else is running his job on that compute node on that particular time (for the same program, same no. of processor, β will vary depending on load of the compute nodes)
- β will go up for high load and go down for small amount of load on the compute nodes
In a typical Distributed Memory network
N processor run time, T(N) = β(N – 1) + 1/N
1 processor run time, T(1) = β(1-1) + 1/1 = 1
Speedup = T(1) / T(N) = 1 /( β(N – 1) + 1/N)
To obtain optimum no. of processor,
Equating ∂T(N)/∂N = 0
=> β – 1/N2 = 0
=> N = β-½
This N is optimum no. of processor for a particular program on a particular time (due to load variation β will vary). Exceeding N will decrease the performance which can be shown as
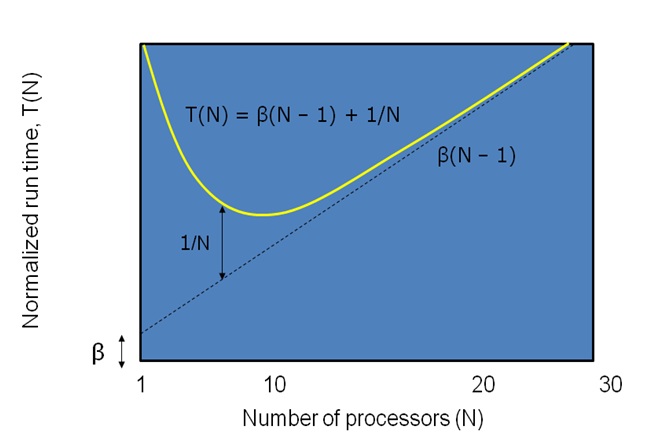
Run time curve
In this case optimum no. of processor is somewhere around 8-10. Executing that program on more than 10 processor will just increase the network overhead and thus increasing the execution time.
Speedup curve can be obtained from that following equation
Speedup = T(1) / T(N) = 1 /( β(N – 1) + 1/N)
= N/( β(N – 1)N + 1)
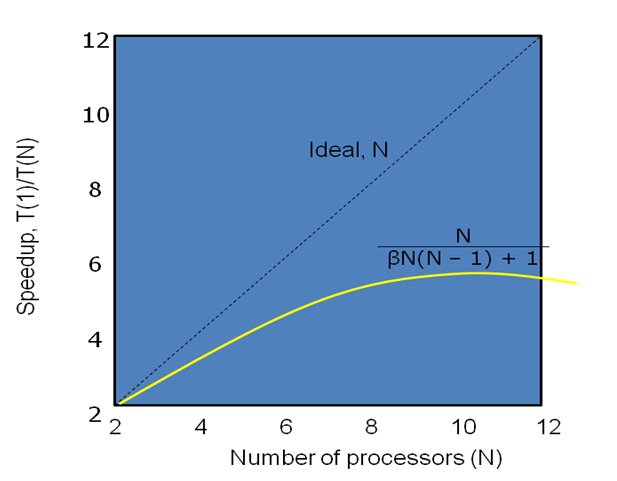
Speedup curve
After reaching a saturation point, that means exceeding optimum no. of processor will decrease maximum speedup.
If you do not have any mathematical model for your program, then we highly encourage you to submit the job asking for 5, 10, 20, 30, 40 processor and so on. Soon you’ll find, for your program there is always an optimum no. of processor. Going beyond that reduces your speedup and takes longer time to execute.
ASKING FOR 100 PROCESSORS DOES NOT MEAN YOUR PROGRAM WILL RUN IN 1 SECOND, IT WILL TAKE LONGER THAN YOU EXPECTED!!
For further details you can visit Dr. Agrawal's website
http://www.eng.auburn.edu/users/agrawvd/COURSE/E6200_Fall10/LECTURES/lec8_Performance.ppt
http://www.eng.auburn.edu/users/agrawvd/COURSE/E6200_Fall10/course.html -> Lecture 8 and subsequent topics



