Aerospace engineering researchers featured on cover of Physics of Fluids
Published: Dec 18, 2020 3:55 PM
By Cassie Montgomery
One hundred years. That’s how long the momentum-integral approach, used to solve all types of boundary layer problems, has been taught to students across the many engineering disciplines that cover fluid mechanics and aerodynamics – from aerospace to mechanical, and passing through civil, biomedical and chemical engineering. Boundary layers exist wherever a solid surface, such as a wing, a rudder, a propeller or an airfoil, comes in contact with a moving fluid, such as a stream of water or air. In short, all wall-bounded flows contain viscous and thermal boundary layers.
History of the Momentum Integral Approach
German physicist Ludwig Prandtl first discovered key boundary layer equations in 1905. His student, Heinrich Blasius, found a clever way to simplify the equations to a numerically solvable form for flow over flat plates, thus introducing the first exact similarity solution for boundary layers in 1908. Thirteen years later, the momentum-integral approach was developed and published concurrently by Hungarian-American aerospace engineer Theodore von Kármán and German mathematician Ernst Pohlhausen in 1921. Von Kármán would later establish the Jet Propulsion Laboratory at the California Institute of Technology, becoming its first chief scientist, and Pohlhausen would move up to become president of Gdansk University of Technology.
The main idea behind the momentum-integral approach is that by inserting Pohlhausen’s guessed polynomials – which could be quadratic, cubic or quartic – into Kármán’s integral equations, several important properties of boundary layers, such as the drag, size and flow separation point, can be estimated. However, this method deteriorates when higher-order Pohlhausen polynomials are used, a paradox that has baffled engineers and scientists for nearly a century.
Joseph Majdalani, professor and Francis Chair of Excellence in the Auburn University Department of Aerospace Engineering, is the latest to improve upon the Kármán-Pohlhausen approach. In collaboration with his postdoctoral scholar, Li-Jun Xuan, Majdalani has recently published a feature cover article in the Physics of Fluids journal explaining the so-called Pohlhausen paradox. Not only have Majdalani and Xuan explained the reason for the paradox, they have discovered an alternative fourth-order polynomial that outperforms Pohlhausen’s by one order of magnitude.
A “perfect” result
“The Blasius equation remains one of the most widely taught nonlinear equations and benchmark problems in fluid mechanics,” Majdalani said. “Through our work, we have extended our understanding of the problem to develop a systematic procedure that leads to a simple, one-term formula that reproduces the Blasius results perfectly. Instead of using computers to discretize it and solve it, we have managed to solve it virtually exactly, with a simple yet highly accurate formula.”
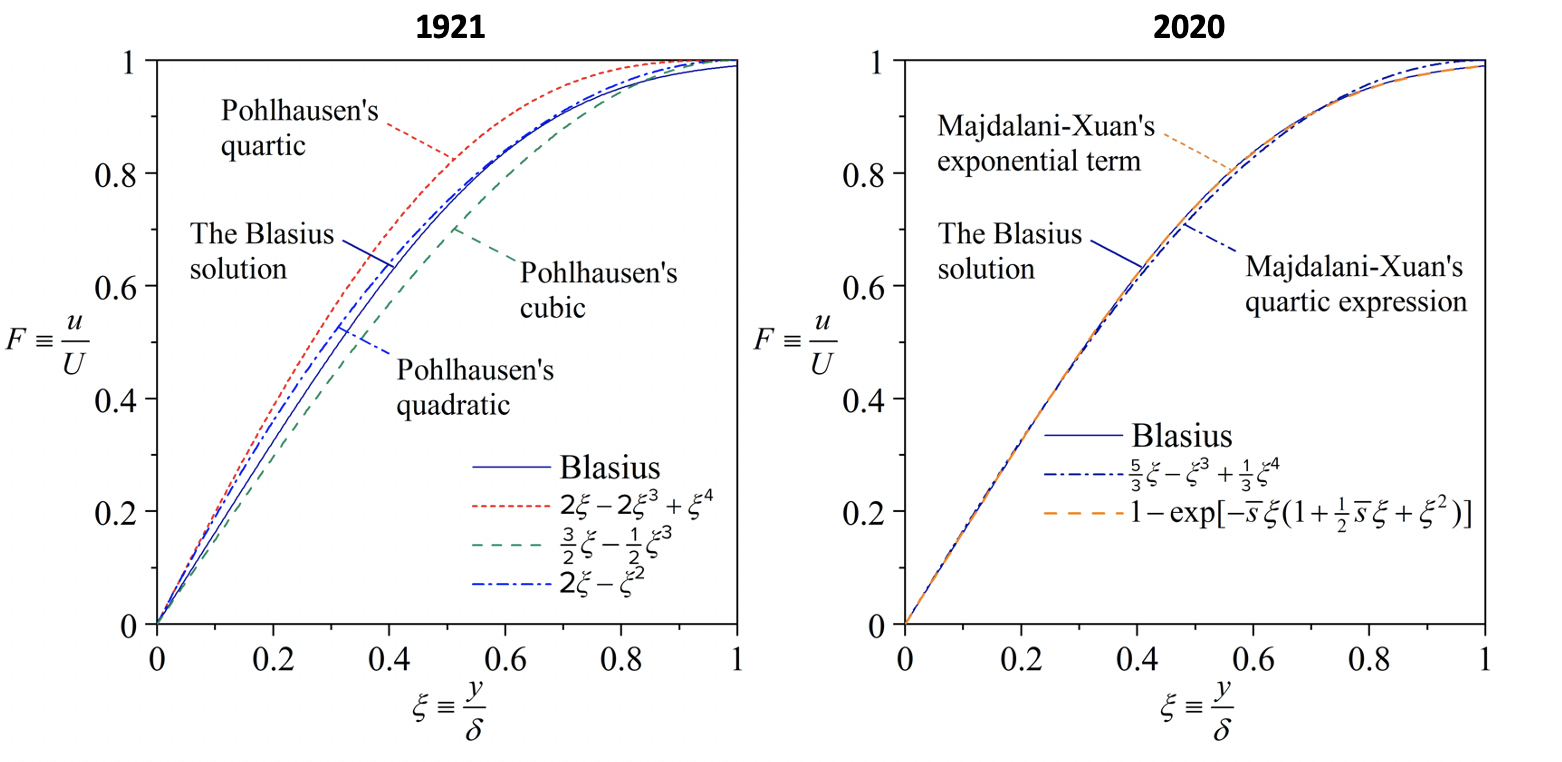
Their results now appear in the fourth edition of the “Viscous Fluid Flow” textbook, co-authored by Frank M. White and Majdalani. In it, “we offer new, highly accurate polynomial approximations that enable us to capture boundary-layer characteristics with virtually zero error,” Majdalani said.
Majdalani explained that the Pohlhausen paradox could be avoided by relaxing one of the five boundary conditions used by Pohlhausen.
“It bothered me when I was a student some 30 years ago and I could not understand for the life of me why in the world, when you use a much longer equation that should be more powerful, you actually get worse results,” he said. “On its centennial anniversary, we now offer a compelling rational explanation for the 1921 Pohlhausen paradox, namely, the reason why the use of a fourth-order, quartic polynomial approximation of the velocity profile in the viscous region leads to less accurate predictions of the skin friction coefficient and disturbance, displacement and momentum thicknesses, than using, for example, quadratic or cubic Pohlhausen polynomials.”
Majdalani and Xuan’s new approach opens up several new lines of research inquiry into analytical solutions to several foundational problems in aerodynamics thought to be unsolvable except numerically.
Media Contact: , cmontgomery@auburn.edu, 334.844.3668



