Xiao Qin's Research

MINT: Mathematical Reliability Models for Energy-Efficient Parallel Disk Systems

2. Findings

2.1 A Reliability Model of Energy-Efficient Parallel Disk Systems with Data Mirroring
2.2 Improving Reliability and Energy Efficiency of Disk Systems via Utilization Control
2.3.1 Framework
2.3.3 Impacts of Temperature on Disk Annual Failure Rate
2.3.4 Power-State Transition Frequency
2.3.5 Single Disk Reliability Model
2.4.1 MAID—Massive Arrays of Idle Disks
2.4.2 PDC—Popular Disk Concentration
2.4.3 Experimental Study on PDC and MAID
2.5.1 Improving Reliability of Cache Disks in MAID via Disk Swapping
2.5.2 Improving Lifetime of MAID System via Disk Swapping
2.5.3 Improving Reliability of PDC via Disk Swapping
2.5.4 Experimental Study on PDC and MAID with Disk Swapping
2.6 Conclusions

2.1 A Reliability Model of Energy-Efficient Parallel Disk Systems with Data Mirroring [6][ Back to Top ]

In the last decade, parallel disk systems have been widely used to support a variety of dataintensive applications running on high-performance computing platforms. The reason behind the popularity of parallel disk systems is that parallel I/O is a promising avenue to bridge the performance gap between processors and I/O systems. For example, redundant arrays of inexpensive disks or RAID can offer high I/O performance with large capacities. The RAID systems improve reliability because they prevent data loss using disk redundancy.

Recent studies show that a significant amount of energy is consumed by parallel disks in high-performance computing centers. Energy conservation in parallel disk systems not only lowers electricity bills, but also leads to reductions of emissions of air pollutants from power generators. Moreover, the storage requirements of modern data-intensive applications and the emergence of disk systems with higher power needs make it desirable to design energy-efficient parallel disk systems. Energy conservation techniques developed for parallel disk systems include dynamic power management schemes, power-aware cache management strategies, power-aware prefetching schemes, and multi-speed settings. Many energy saving techniques significantly conserve energy in parallel disk systems at the apparent cost of reliability. Even worse, a parallel disk system consisting of multiple disks has a higher failure rate compared with a larger single disk system. This is due to the fact that there are more components in the parallel disk system. Due to hardware and software defects, failed components in a parallel disk system can ultimately cause failures in the system at run-time. In addition to the energy efficiency issue, fault tolerance and reliability are major concerns in the design of modern parallel disk systems. These disk systems are expected to be the most stable part of high-performance computing systems. Therefore, it is not surprising that academic institutes, industry, and government agencies consider the reliability and energyefficiency of parallel disks in their computing systems essential and critical to operations. The long-term goal of this research is to develop novel energy conservation schemes with marginal adverse impacts on the reliability of parallel disk systems. To achieve this longterm objective, in this study we investigate fundamental theories to model the reliability of energy-efficient parallel disk systems using data mirroring.

In this study we present a quantitative approach to addressing the issue of conserving energy without noticeably degrading reliability of parallel disk systems. We focus on parallel disk systems with data mirroring, which is a technique for maintaining two or more identical disk images on multiple disk devices. The data mirroring technique leverages redundant data to significantly enhance reliability. Among the various energy conservation techniques, we focus on a widely adopted technique dynamic power management, which dynamically changes the power state of disks. The dynamic power management technique turns disks into low-power states (e.g., sleep state) when the disk I/O workload is fairly light. In this study, we use a Markov process to develop a quantitative reliability model for energy-efficient parallel disk systems with data mirroring. Next, we evaluate the reliability and energy efficiency of parallel disk systems using the new reliability model. Furthermore, using the Weibull distribution to model disk failure rates, we analyze the reliability of a real-world parallel disk system. Finally, we propose a method capable of obtaining a balance between the reliability and energy efficiency of parallel disk systems with data mirroring.

With our novel reliability model in place, it becomes feasible to devise new approaches to seamlessly integrate energy efficiency and fault tolerance. The goal of these approaches is to provide significant energy savings, while ensuring high reliability for parallel disk systems without sacrificing performance. Our approach has several advantages over traditional qualitative approaches. This is because our model not only can quantify the reliability of energy-efficient parallel disks, but also can be used to balance energy efficiency and reliability.

2.2 Improving Reliability and Energy Efficiency of Disk Systems via Utilization Control [1][ Back to Top ]

Disk drives started the new era in the computer dictionary. Therefore, it is crucial to have highly reliable, energy efficient and cost effective disks. Extensive research has been done (and continues to be done) to reduce the energy consumption of disks. Literature proves that very little or no research has been done to maximize reliability and energy efficiency of the disks. Reliability may be the most important characteristic of the disk drives if the data stored on the disk drives is mission critical. Disk drives are generally very reliable but may fail. In this paper disk age and utilization are studied as the major factors that affect disk drive reliability. In this paper we studied the failure probabilities with respect to disk age and utilization. This relationship is made explicit in the form of graphs. These graphs are used to estimate safe utilization levels for disks of differing ages. Safe utilization zones are the range of utilization levels where the probabilities of disk failures are minimal. Simulations prove that when disks are operated in the safe utilization zones, the probabilities of failures are effectively minimized.

It is evident that disk drives consume large amounts of energy. Reducing the energy consumption not only lowers electricity bills but also tremendously reduces the emissions of air pollutants. Energy consumption is reduced by operating the disks at three power modes: Active, Idle and Sleep. Mirroring disks (a.k.a., RAID1) is considered for the experiments, which uses a minimum of two disks; one primary and one back up. The data is mirrored to the backup disk from the primary disk. Traditional methods wake up the backup disk when the utilization of the primary disk exceeds 100 percent. Load balancing technique keeps both the primary and back up disks always active to share the load. These methods consume a massive amount of energy, as the disks stay active even when there are no requests to serve for a long period of time. The reliability of these disks is also ignored most of the time. We designed a policy where we operate the disks at different power modes based on the utilization of the disk. The utilization of the disk is calculated a priori. Along with the power conservation we also aim at achieving high reliability. Thus, we must operate the disks only in safe utilization zones.

In the policy we defined, the processor generates the read requests that should be processed by the disks. These read requests are queued up in a buffer and the utilization levels are calculated. These utilization levels are checked against the limits of the safe utilization zone and then the disk modes are changed accordingly. This approach is not only reliable but also saves a significant amount of energy. This approach saves more energy for Travelstar disks when compared with Ultrastar disks, because the energy levels of the disk parameters like spin up, spin down, active power, idle power and etc. are much higher for Ultrastar disks when compared to Travelstar disks. It should be noted here that the disk parameters play a major role in the energy consumption of the disk.

2.3 The MINT Reliability Model

2.3.1 Framework[ Back to Top ]

Fig. 1 depicts the framework of the MINT reliability model for parallel disk systems with energy conservation schemes. MINT is composed of a single disk reliability model, a systemlevel reliability model, and three reliability-affecting factors - temperature, disk state transition frequency (hereinafter referred to as frequency) and utilization. Many energy-saving schemes (e.g., PDC [4] and MAID [2]) inherently affect reliability-related factors like disk utilization and transition frequency. Given an energy optimization mechanism, MINT first transfers data access patterns into the two reliability-affecting factors - frequency and utilization. The single-disk reliability model can derive individual disk’s annual failure rate from utilization, power-state transition frequency, age, and temperature. Each disk’s reliability is used as input to the system-level reliability model that estimates the annual failure rate of parallel disk systems.

For simplicity without losing generality, we consider four reliability-related factors in MINT. This assumption does not necessarily indicate that disk utilization, age, temperature,

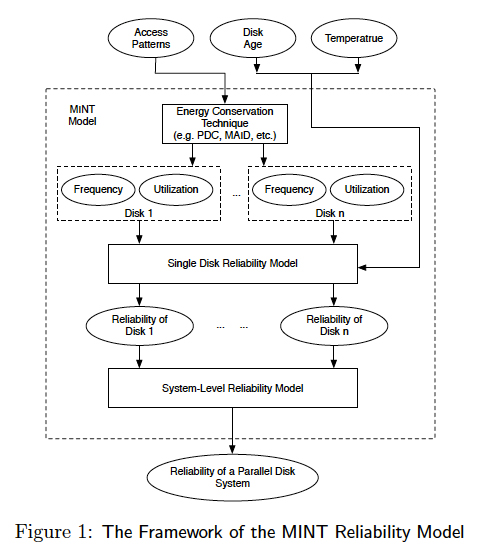
and power-state transitions are the only parameters affecting disk reliability. Other factors having impacts on reliability include handling, humidity, voltage variation, vintage, duty cycle, and altitude [3]. If a new factor has to be integrated into MINT, we can extend the single reliability model described in Section 2.3.5. Since the infant mortality phenomena is out the scope of this study, we pay attention to disks that are more than one year old.

2.3.2 Impacts of Utilization on Disk Annual Failure Rate[ Back to Top ]

Disk utilization can be characterized as the fraction of active time of a disk drive out of its total powered-on-time [5]. In our single disk reliability model, the impacts of disk utilization on reliability is good way of providing a baseline characterization of disk annual failure rate (AFR). Using field failure data collected by Google, shows the impact of utilization on AFR across the different age groups. Pinheiro et al. studied the impact of utilization on AFR accross different disk age groups. Pinheiro et al. categorized disk utilization in three levels - low, medium, and high. Fig. 2 shows AFRs of disks whose ages are 3 months, 6 months, 1 year, 2 years, 3 years, 4 years, and 5 years under the three utilization levels. Since the singledisk reliability model needs a baseline AFR derived from a numerical value of utilization, we make use of the polynomial curve-fitting technique to model the baseline value of a single disk’s AFR as a function of utilization. Thus, the baseline value (i.e., BaseV alue in Eq. 2.4) of AFR for a disk can be calculated from the disk’s utilization. Fig. 3 shows the AFR value of disks, the ages of which is 3-year, as a function of its utilization. The curve plotted in Fig. ?? can be modeled as a utilization-reliability function described as Eq. 2.1 below:

where R(u) represents the AFR value as a function of a certain disk utilization u. With Eq. 2.1 in place, one can readily derive annual failure rate of a disk if its age and utilization are given. For example, for a 3-year old disk with 50% utilization (i.e., u = 50%), we can obtain the AFR value of this disk as R(u) = 4.8%. Fig. 3 suggests that unlike the conclusions

drawn in a previous study (see [7]), a low disk utilization does not necessarily lead to low AFR. For instance, given a 3-year old disk, the AFR value under 30% utilization is even higher than AFR under 80% utilization.

2.3.3 Impacts of Temperature on Disk Annual Failure Rate[ Back to Top ]

Temperature is often considered as the most important environmental factor affecting disk reliability. Field failure data of disks in a Google data center (see Fig. 4) shows that in most cases when temperatures are higher than 35◦C, increasing temperatures lead to an increase in disk annual failure rates. On the other hand, Fig. 4 indicates that in the low and middle temperature ranges, the failure rates decreases when temperature increases [5].

Growing evidence shows that disk reliability should reflect disk drives operating under environmental conditions like temperature [3]. Since temperature (e.g., meaured 1/2” from the case) apparently affect disk reliability, the temperature can be considered as a multiplier (hereinafter referred to as temperature factor) to baseline failure rates where environmental factors are integrted [3]. Given a temperature, one must decide the corresponding temperature factor (see TemperatureF actor in Eq. 2.4) that can be multiplied to the base failure rates. Using Google’s field failure data plotted in 4, we attempted to calculate temperature factors under various temperatures ranges for disks with different ages. More specifically, Fig. 4 shows annual failure rates of disks whose ages are from 3-month to 4-year old. For disk drives whose ages fall in each age range, we model the temperature factor as a function of drive temperature. Thus, six temperature-factor functions must be derived.

Now we explain how to determine a temperature facotr for each temperature under each age range. Let us choose 25◦C as the base temperature value, because room temperatures of data centers in many cases are set as 25◦C controlled by cooling systems. Thus, the temperature factor is 1 when temperature is set to the base temperature - 25◦C. Let T denote the average temperature, we define the temperature factor for temperature T as T/25 if T is larger than 25◦C. When T exceeds 45◦C, the temperature factor becomes a constant (i.e., 1.8 = 45/25). Due to space limit, we only show how temperature affects the temperature factor of a 3-year old disk in Fig. 4. Note that the temperature-factor functions for disks in other age ranges can be modeled in a similar way. Fig. 5 shows the temperature factor function derived from Fig. 4 for 3-year old disks. We can observe from Fig. 4 that AFRs increase to 215% of the base value when the temperature is between 40 to 45◦C.

2.3.4 Power-State Transition Frequency[ Back to Top ]

To conserve energy in single disks, power management policies turn idle disks from the active state into standby. The disk power-state transition frequency (or frequency for short) is often measured as the number of power-state transitions (i.e., from active to standby or vice versa) per month. The reliability of an individual disk is affected by power-state transitions and; therefore, the increase in failure rate as a function of power-state transition frequency has to be added to a baseline failure rate (see Eq. 2.4 in Section 2.3.5). We define an increase in AFR due to power-state transitions as power-state transition frequency adder (frequency adder for short). The frequency adder is modeled by combining the disk spindle start/stop failure rate adders described by IDEMA [7] and the PRESS model [8]. Again, we focus on 3- year old disk drives. Fig. 6 demonstrates frequency adder values as a function of power-state transition frequency. Fig. 6 shows that high frequency leads to a high frequency adder to be added into the base AFR value. We used the quadratic curve fitting technique to model the frequency adder function (see Eq. (2.3)) plotted in Fig. 6.

where f is a power-state transition frequency, R(f) represents an adder to the base AFR value. For example, suppose the transition frequency is 300 per month, the base AFR value needs to be increase by 1.33%.

2.3.5 Single Disk Reliability Model[ Back to Top ]

Single-disk reliability can not be accurately described by one valued parameter, because the disk drive reliability is affected by multiple factors (see Sections 2.3.2,2.3.3, and 2.3.4). Though recent studies attempted to consider multiple reliability factors (see, for example, PRESS [8]), few of prior studies investigated the details of combining the multiple reliability factors. We model the single-disk reliability in terms of annual failure rate (AFR) in the following three steps. We first compute a baseline AFR as a function of disk utilization. We then use temperature factor as a multiplier to the baseline AFR. Finally, we add a powerstate transition frequency adder to the baseline value of AFR. Hence, the failure rate R of an individual disk can be expressed as:

where BaseV alue is the baseline failure rate derived from disk utilization (see Section 2.3.2), TemperatureF actor is the temperature factor (or temperature multiplier; see Section 2.3.3), FrequencyAdder is the power-state transition frequency adder to the base AFR (see Section 2.3.4), and α and β are two coefficients to reliability R. If reliability R is more sensitive to frequency than to utilization and temperature, then β must be greater than α. Otherwise, β is smaller than α. In either cases, α and β can be set in accordance with R’s sensitivities to utilization, temperature, and frequency. In our experiments, we assume that all the three reliability-related factors are equally important (i.e., α=β=1). Ideally, extensive field tests allow us to analyze and test the two coefficients. Although α and β are not fully evaluated by field testing, reliability results are valid because of the following two reasons: first, we have used the same values of α and β to evaluate impacts of the two energy-saving schemes on disk reliability (see Section ??); second, the failure-rate trend of a disk when α and β are set to 1 are very similar to those of the same disk when the values of α and β do not equal to 1.

With Eq. 2.4 in place, we can analyze a disk’s reliability in turns of annual failure rate (AFR). Fig. 7 shows AFR of a three-year-old disk when its utilization is in the range between 20% and 80%. We observe from Fig. 7 that increasing temperature from 35◦C to 40◦C gives rise to a significant increase in AFR. Unlike temperature, power-state transition frequency in the range of a few hundreds per month has marginal impact on AFR. It is expected that when transition frequency is extremely high, AFR becomes more sensitive to frequency than to temperature.

2.4 Reliability Model for MAID and PDC

2.4.1 MAID—Massive Arrays of Idle Disks[ Back to Top ]

Background The MAID (Massive Arrays of Idle Disks) technique—developed by Colarelli and Grunwald—aims to reduce energy consumption of large disk arrays while maintaining acceptable I/O performance [2]. MAID relies on data temporal locality to place replicas of active files on a subset of cache disks, thereby allowing other disks to spin down. Fig. 8 shows that MAID maintains two types of disks - cache disks and data disks. Popular files are copied from data disks into cache disks, where the LRU policy is implemented to manage data replacement in cache disks. Replaced data is discarded by a cache disk if the data is clean; dirty data has to be written back to the corresponding data disk. To prevent cache disk from being overly loaded, MAID avoids copying data to cache disks that have reached their maximum bandwidth. Three components integrated in the MAID model include: (1) power management policy, by using which drives that have not seen any requests for a specified period are spun down to sleep, or an adaptive spin-down to active; (2) data layout, which is either linear, with successive blocks being placed on the same drive, or striped across multiple drives; (3) cache, which indicates the number of drives of the array which will be used for cache [2].

Modeling Utilization of Disks in MAID Recall that the annual failure rate of each disk can be calculated using disk age, utilization, operating temperature as well as power state transition frequency. To model reliability of a disk array equipped with MAID, we have to first address the issue of modeling disk utilization used to calculate base annual failure rates. In this subsection, we develop a utilization model capturing behaviors of a MAID-based disk array. The utilization model takes file access patterns as an input and calculates the utilization of each disk in the disk array.

Disk utilization is computed as the fraction of active time of a disk drive out of its total powered-on-time. Now we describe a generic way of modeling the utilization of a disk drive. Let us consider a sequence of I/O accesses with N I/O phases. We denote Ti as the length or duration of the ith I/O phase. Without loss of generality, we assume that a file access pattern in an I/O phase remains unchanged. The file access pattern, however, may vary in different phases. The relative length or weight of the ith phase is expressed as Wi = Ti/T where is the total length of all the I/O phases. Suppose the utilization of a disk in the ith phase is ρi, we can write the overall utilization ρ of the disk as the weighted sum of the utilization in all the I/O phases. Thus, we have

Let Fi = (fi1, fi2, ..., fini) be a set of ni files residing in the disk in the ith phase. The utilization ρi (see Eq. 2.5) of the disk in phase i is contributed by I/O accesses to each file in set Fi. Thus, ρi in Eq. 2.5 can be written as:

where λij is the file access rate of file fij in Fi and sij is the mean service time of file fij. Note that I/O accesses to each file in set Fi are modeled as a Poisson process; file access rate and service time in each phase i are given a priori. We assume that there are n hard drives with k phases. In the l-th phase, let fijl be the j-th file on the i-th disk, where i ∈ (1, 2, · · · , n), j ∈ (1, 2, · · · ,mi), l ∈ (1, 2, · · · k). We have:

where mi is the number of files on the ith disk and Fil is the total files on the same disk. Since frequently accessed files are duplicated to cache disks, we model below an updated file placement after copying the frequently accessed files.

where m'i is the number of the files on the i-th disk, f'ijl is the j-th file at the l-th phase and F'il is the set of files on the same disk after the files are copied. We can calculate the utilization for j-th file in the lth phase on the i-th disk as

We assume that ρi1l ≥ ρi2l ≥ · · · ≥ ρim1l, meaning that files are placed in a descending order of utilization. After the frequently accessed files are copied to the cache disks, we denote the updated utilization contributed by files including copied ones as ρ'i1l≥ ρ'i2l≥ · · · ≥ρ'im1l. It is intuitive that the utilization of disk i should be smaller than 1. When a disk reaches its maximum utilization, the disk also reaches its maximum bandwidth denoted as Bi. Regardless of cache disks or data disks, we express the utilization for i-th disk in phase l as:

where T is the time interval of the lth I/O phase. The first and second items on the bottom-line on the right-hand side of Eq. 2.10 are the utilizations caused by accessing files and duplicating files from data disks to cache disks, respectively.

Since files on cache disks are duplicated from data disks, frequently accessed files must be copied from data disks and written down to cache disks. As such, we must consider disk utilization incurred by the data duplication process. To quantify utilization overhead caused by data replicas, we define a set of files copied from the ith data disk to cache disks in phase l. Similarly, we define a set of files copied to the ith cache disk from data disks in phase l.

At the lth phase, the file fijl, which is the jth file on the ith disk will be copied out of the data disk if its utilization ρijl is higher than ρi1l, which is the highest utilization held by file fi1l. For all files to be copied out on the ith disk can be expressed as

With respect to the ith data disk, the utilization ρ' il−data in phase l is the sum of utilization caused by accessing files on the data disk and reading files to be duplicated to cache disks. Thus, ρ'il−data can be written as:

where the first and second items on the right-hand side of Eq. 2.12 are the utilizations of accessing files and reading files from the data disk to make replicas on cache disks, respectively.

When it comes to the ith cache disk, the utilization ρ'il−cache in phase l is the sum of utilization contributed by accessed files and written file replicas to cache disks. Thus, ρ'il−data can be written as:

where the first and second items on the right-hand side of Eq. 2.13 are the utilizations of accessing files and writing files to the cache disk to make replicas, respectively.

Modeling Power-State Transition Frequency for MAID Eq. 2.4 in Section 2.3.5 shows that the power-state transition frequency adder is an important factor to model disk annual failure rate. The number of power-state transitions largely depends on I/O workload conditions in addition to the behaviors of MAID. In this subsection, we derive the number of power-state transitions from file access patterns.

We define the TBE as the disk break-even time - the minimum idle time required to compensate the cost of entering the disk standby mode (TBE values are usually anywhere between 10 to 15 seconds). Given file access patterns of the ith phase for a disk, we need to calculate the number τi of idle periods that are larger than the break-even time TBE. The number of power-state transitions during phase i is 2τi, because there is a spin-down at the beginning of each large idle time and a spin-up by the end of the idle time. For an access pattern with N I/O phases, the total number of power-state transitions τ can be expressed as:

We model a workload condition where I/O burstiness can be leveraged by the dynamic power management policy to turn idle disks into the standby mode to save energy. To model I/O burstiness, we assume the first I/O requests of files within an access phase are arriving in a short period of time, within which disks are too busy to be switched into standby. After the period of high I/O load, there is an increasing number of opportunities to place disks into the standby mode. This workload model allows MAID to achieve high energy efficiency at the cost of disk reliability, because the workload model leads to a large number of power-state transitions.

To conduct a stress test on reliability of MAID, we assume that the first requests of files on a disk arrive at the same time. For the first few time units, the workloads are so high that no data disks can be turned into standby. As the I/O load is descreasing, some data disks may be switched to standby when idle time intervals are larger than TBE. In this workload model, MAID can achieve the best energy efficiency with the worst reliability in terms of the number of power-state transitions.

Let us model power-state transition frequency for a single disk. Assume that the hi-th file (hi is placed in an decending order from mi, hi ∈ (mi,mi−1, . . . , 2, 1)) on the i-th disk at the l-th phase is the dividing point of the request access rate. Given a file whose index is larger than hi, the file’s access rate λijl enables the disk to be turned in standby because idle times are larger than break-even time TBE. Hence, we have:

where is the interval time of the first file on the ith disk. The number of the spin ups/downs is 2(T · λi1l − T · λihil). Cache disks in MAID are very unlikely to be switched into the standby mode. Since cache disks store replicas, any failure in the cache disks has no impact on data loss. Only failures in data disks affect the reliability of disk arrays.

2.4.2 PDC—Popular Disk Concentration[ Back to Top ]

Background The PDC (Popular Data Concentration) technique proposed by Pinheiro and Bianchini migrates frequently accessed data to a subset of disks in a disk array [4]. Fig. 9 demonstrates the basic idea behind PDC: the most popular files are stored in the far left disk, while the least popular files are stored in the far right disk. PDC can rely on file popularity and migration to conserve energy in disk arrays, because several network servers exhibit I/O loads with highly skewed data access patterns. The migrations of popular files to a subset

of disks can skew disk I/O load towards this subset, offering other disk more opportunities to be switched to standby to conserve energy. To void performance degradation of disks storing popular data, PDC aims at migrating data onto a disk until its load is approaching the maximum bandwidth of the disk.

The main difference between MAID and PDC is that MAID makes data replicas on cache disks, whereas PDC lays data out across disk arrays without generating any replicas. If one of the cache disks fails in MAID, files residing in the failed cache disks can be found in the corresponding data disks. In contrast, any failed disk in PDC can inevitably lead to data loss. Although PDC tends to have lower reliability than MAID, PDC does not need to trade disk capacity for improved energy efficiency and I/O performance.

Modeling Utilization of Disks in PDC Since frequently accessed files are periodically migrated to a subset of disks in a disk array, we have to take into account disk utilization incurred by file migrations. Hence, the ith disk’s utilization ρ'il during phase l is computed as the sum of the utilization contributed by accessing files residing in disk i and the utilization introduced by migrating files to/from disk i. Thus, we can express utilization ρ'il as:

where T is the time interval of I/O phase l. The first and second items on the bottom-line on the right-hand side of Eq. 2.16 are the utilizations caused by accessing files and duplicating files from data disks to cache disks, respectively.

To quantify utilization introduced by the file migration process (see the second item on the bottom-line on the right-hand side of Eq. 2.16), we define two set of files for the ith disk in the lth I/O phase. The first set contains all the files migrated from disk i to other disks during the lth phase. Similarly, the second set consists of files migrated from other disks to disk i in phase l.

Now we can formally express the utilization of disk i in phase l using the two file sets and . Thus, we have:

where the second item on the right-hand side of Eq. 2.17 is the utilization incurred by (1) migrating files in set from disk i to other disks and (2) migrating files in set from other disks to disk i during phase l.

Modeling Power-State Transition Frequency for PDC We used the same way described in Section 2.4.1 to model power-state transition frequency for PDC. The transition frequency plays a critical role in modeling reliability, because the frequency adder to base AFRs is derived from the transition frequency measured in terms of the number of spin-ups and spin-downs per month. Unlike MAID, PDC allows each disk to receive migrated data from other disks. In light of PDC, disks storing the most popular files are most likely to be kept in the active mode.

2.4.3 Experimental Study on PDC and MAID [ Back to Top ]

Experimental Setup We developed a simulator to valid the reliability models for MAID and PDC. We considered two approaches to configuring MAID. In the first approach, extra cache disks are added to a disk array to cache frequently accessed data. In the second one,we make use of existing data disks as cache disks. We analyze the reliability of the two different MAID configurations. Table 1 shows the parameters of configurations for MAID and PDC. In the first configuration or MAID-1 (shown as MAID-1 in Table 1), there are 5 cache disks and 20 data disks. In the second configuration or MAID-2 (shown as MAID-2 in Table 1), there are 5 cache disks and 15 data disks. For the case of PDC, we set the number of disks to 20. Thus, MAID-2 and PDC have the same number of disks whereas MAID-1 has five extra cache disks. The file access rate is in the range from 0 to 500 No./month. The operating temperature is set to 35◦C.

Preliminary Results We first investigate the impacts of file access rate on utilization of MAID and PDC. Fig. 10 shows that when the average file access rate increases, the utilizations of PDC, MAID-1, and MAID-2 increase accordingly. Compared with the utilizations of MAID-1 and MAID-2, the utilization of PDC is a whole lot more sensitive to the file access rate. Moreover, the utilization of PDC is significantly higher than those of MAID-1 and MAID-2. For example, when the average file access rate is 5∗105 No./month, the utilizations of PDC, MAID-1, and MAID-2 are approaching to 90%, 48%, and 40%, respectively. PDC has high utilization, because disks in PDC spend noticeable amount of time in migrating data among the disks. Increasing the file access rate leads to an increase in the number

Figure 10: Impacts of File Access Rate on Utilization
Access Rate is increased from 10 to 50 ∗ 103 No./month

of migrated files among the disks, thereby giving rise to an increased utilization due to file migrations. Unlike PDC, MAID-1 and MAID-2 simply needs to make replicas on cache disks without migrating the replicas back from the cache disks to data disks.

Under low I/O load, the utilizations of MAID-1 and MAID-2 are very close to each other. When I/O load becomes relatively high, the utilization of MAID-1 is slightly higher than that of MAID-2. This is mainly because the capacity of MAID-2 is larger than that of MAID-1.

Fig. 11 shows the annual failure rates or AFR of MAID-1, MAID-2, and PDC.We observe from Fig. 11 that the AFR value of PDC keeps increasing from 5.6% to 8.3% when the file access rate is larger than 150. We attribute this trend to high disk utilization due to data migrations. More interestingly, if the file access rate is lower than 15 ∗ 104, AFR of PDC slightly reduces from 5.9% to 5.6% when the access rate is increased from 5 ∗ 105 to 15 ∗ 104. This result can be explained by the nature of the utilization function that is concave rather than linear. The concave nature of the utilization function is consistent with the empirical results reported in [5]. When the file access rate 15∗104, the disk utilization is approximately 50%, which is the turing point of the utilization function.

Figure 11: Impacts of File Access Rate on Annual Failure Rate (AFR) of PDC, MAID-1, and MAID-2 Access Rate is increased from 10 to 50 ∗ 103 No./month

Figure 12: Impacts of File Access Rate on Utilization
Access Rate is increased from 10 to 10 ∗ 105 No./month

Unlike the AFR of PDC, the AFRs of MAID-1 and MAID-2 continue decreasing from 6.3% to 5.8% with the increasing file access rate. This declining trend might be explained by two reasons. First, increasing the file access rates reduces the number of power-state transitions. Second, the range of the disk utilization is close to 40%, which is in the declining part of the curve.

Now we conduct a stress test by further increasing the average file access rate from 5 ∗ 105 to 10 ∗ 105 No./month. Interestingly, we observe from experimental results that the utilization trends and AFR trends of PDC and MAID plotted in Figs. 12 and 13 are different from the trends of utilization and AFR plotted in Figs. 10 and 11. More specifically, Fig. 12 shows that the utilization of PDC is saturated at the level of 90% after the average file access rate exceeds 5 ∗ 105 No./month. In contrast, the utilizations of both MAID-1 and MAID2 continue increasing with an increase in the average file access rate. Regardless of the value of access rate, the growing trends in utilization are consistantly true for MAID-1 and MAID-2 even when the access rate is larger than 5 ∗ 105 No./month. The PDC’s utilization almost becomes a constant when the access rate is larger than 5 ∗ 105 No./month, because the high access rate can easily saturate the bandwidth of disks storing popular files. After the hot disks are saturated, the utilization caused by file migrations is significantly decreasing as the number of file migrations drops. When the access rate approaches 10 ∗ 105, the utilization of MAID-1 becomes significantly higher than that of MAID-2. The utilization of MAID-1 grows faster than that of MAID-2, because MAID-2 has more data disks than MAID-1.

Figure 13: Annual Failure Rate (AFR) of PDC, MAID-1/MAID-2
Access Rate is increased from 10 to 10 ∗ 105 No./month

Figs. 13 shows the annual failure rates (AFRs) of PDC and MAID-1/MAID-2 as functions of file access rate when temperature is set to 35◦C. The first observation drawn drawn from Figs. 13 is that the AFR value of PDC only slightly increases after the average file access rate exceeds 500 per month. PDC’s AFR grows very slowly under high I/O load because the utilizations of disks in PDC are almost saturated at the level of 90% when the access rate is higher than 500. More importantly, the second observation concluded from Figs. 13 is that when the access rate is higher than 7 ∗ 105 No./month, AFR of MAID-1 is higher than that of MAID-2. The main reason is that MAID-2 has five more data disks compare to MAID-1 which ensures that the utilization MAID-2 will be lower than MAID-1. The utiliaztion of MAID-1 keeps rising up over 60% (see Fig. 12) when access rate is higher than 7 ∗ 105 No./month while at the same time the utilization of MAID-2 is around 50% which lies in the lowest point of the AFR-Utilization curve shown in Fig. 3.

2.5 MAID and PDC via Disk Swapping

2.5.1 Improving Reliability of Cache Disks in MAID via Disk Swapping[ Back to Top ]

Cache disks in MAID are more likely to fail than data disks due to the two reasons. First, cache disks are always kept active to maintain short I/O response times. Second, the utilization of cache disks is expected to be much higher than that of data disks. From the aspect of data loss, the reliability of MAID relies on the failure rate of data disks rather than that of cache disks. However, cache disks tend to be a single point of failure in MAID, which if the cache disks fail, will stop MAID from conserving energy. In addition, frequently replacing failed cache disks can increase hardware and management costs in MAID. To address this single point of failure issue and make MAID cost-effective, we designed a disk swapping strategy for enhancing the reliability of cache disks in MAID.

Figure 14: Disk Swapping in MAID: The two cache disks on the left-hand side are swapped with the two data disks on the right-hand side.

Fig. 14 shows the basic idea of the disk swapping mechanism, according to which disks rotate to perform the cache-disk functionality. In other words, the roles of cache disks and data disks will be periodically switched in a way that all the disks in MAID have equal chance to perform the role of caching popular data. For example, the two cache disks on the left-hand side in Fig. 14 are swapped with the two data disks on the right-hand side after a certain period of time. For simplicity without losing generality, we assume that all the data disks in MAID initially are identical in terms of reliability. This assumption is reasonable because when a MAID system is built, all the new disks with the same model come from the same vendor. Initially, the two cache disks in Fig. 14 can be swapped with any data disk. After the initial phase of disk swapping, the cache disks are switched their role of storing replica data with the data disks with the lowest annual failure rate. In doing so, we ensure that cache disks are the most reliable ones among all the disks in MAID after each disk swapping process. It is worth noting that the goal of disk swapping is not to increase mean time to data loss, but is to boost mean time to cache-disk failure by balancing failure rates across all disks in MAID.

Disk swapping is advantageous to MAID, and the reason is two-fold. First, disk swapping further improves the energy efficiency of MAID because any failed cache disk can prevent MAID from effectively saving energy. Second, disk swapping reduces maintenance cost of MAID by making cache disks less likely to fail.

2.5.2 Improving Lifetime of MAID System via Disk Swapping[ Back to Top ]

When we study the reliability above, the MTTDL(a.k.a mean time to data loss) is the basic principle to define the failure of the storage system. According to MTTDL, the system won’t be treated as fail so long as the system still holds the data. In this case, even the cache disks in the MAID which only hold the replicas of hot data fail, the whole system still can provide the data services thoroughly. However, after the failure of cache disks, the whole system will suffer from the low energy efficiency since the data disks which are supposed to be spun down to save energy have to be spun up to provide the data services. Furthermore, the system will also suffer from the low performance due to the time delay caused by the disks state transition from spun down to spun up. Last but not the least, changing the failed cache disks will increase the maintenance fee of MAID.

Figure 15: PDC-Swap1- the first disk-swapping strategy in PDC: the ith most popular disk is swapped with the ith least popular disk.

Hence, we introduce another definition of reliability to MAID system called MTTF(a.k.a mean time to fail) [5]. The main difference between the idea of MTTDL and MTTF for MAID is that MTTDL only considers the data disks’ error as the failure of systems while MTTF treats the error of any disks as the failure of systems no matter they are cache disks or data ones. In this case, the failure of the cache disks will also be treated as the MAID systems’ failure.

2.5.3 Improving Reliability of PDC via Disk Swapping[ Back to Top ]

Compared with disks storing popular files (hereinafter referred to as popular disks), disks archiving non-popular files tend to have lower failure rates because the utilization of popular disks is significantly higher than that of non-popular disks. In other words, popular disks have high chance of staying active serving I/O requests that access popular files, whereas non-popular disks are likely to be placed in the standby mode to conserve energy. Frequently repairing failed popular disks results in the following two adverse impacts. First, replacing failed hard drives with new ones can increase the overall hardware maintenance cost in PDC. Second, restoring disk data objects incurs extra energy overhead, thereby reducing the energy efficiency of PDC. To address these two problems of frequent repairing popular disks, we developed two disk-swapping strategies to improve the reliability of popular disks in PDC. Fig. 15 shows the first disk-swapping strategy tailored for PDC. In this strategy called PDC-Swap1, the most popular disk is swapped with the least popular disk; the second most popular one is swapped with the second least popular disk; and the ith most popular disk is swapped with the ith least popular disk. Although the PDC-Swap1 is a straightforward approach, it does not necessarily lead to a balanced failure rates across all the disks in PDC. This is mainly because the graphs of AFR-utilization functions (see, for example, Fig. 7) are U-shaped curves, indicating that low disk utilization does not necessarily result in low annual failure rate (AFR). A potential disadvantage of the PDC-Swap1 strategy lies in the possibility that PDC-Swap1 is unable to noticeably improve the reliability of PDC. Such a disadvantage may occur when the utilization of the non-popular disks is so low that their AFRs are as high as those of popular disks.

Figure 16: PDC-Swap2 - The second disk-swapping strategy in PDC: the ith most popular disk is swapped with another disk with the ith lowest annual failure rate.

To solve the above potential problems of PDC-Swap1, we proposed a second disk swapping strategy in PDC. Fig. 16 outlines the basic idea of the second disk-swapping strategy called PDC-Swap2, which attempts to switch the most popular disk with the one with the lowest AFR. In general, PDC-Swap2 switches the ith most popular disk with another disk with the ith lowest AFR. The PDC-Swap2 strategy guarantees that after each swapping procedure, disks with low failure rates start serving as popular disks. Unlike PDCSwap1, PDC-Swap2 can substantially improve the reliability of PDC by balancing the failure rates across all the popular and non-popular disks.

2.5.4 Experimental Study on PDC and MAID with Disk Swapping[Back to Top]

Preliminary Results A key issue of the disk-swapping strategies is to determine circumstances under which disks should be swapped in order to improve disk system reliability. One straightforward way to address this issue is to periodically initiate the disk-swapping process. For example, we can swap disks in MAID and PDC once every year. Periodically swapping disks, however, might not always enhance the reliability of parallel disk systems. For instance, swapping disks under very light workloads cannot substantially improve disk system reliability. In some extreme cases, swapping disks under light workload may worsen disk reliability due to overhead of swapping. As such, our disk-swapping strategies do not periodically swap disks. Rather, the disk-swapping process is initiated when the average I/O access rates exceed a threshold. In our experiments, we evaluated the impact of this accessrate threshold on the reliability of a parallel disk system. More specifically, the threshold is set to 2 ∗ 105, 5 ∗ 105, and 8 ∗ 105 times/month, respectively. These three values are representative values for the threshold, because when the access rate hits 5 ∗ 105, the disk utilization lies in the range between 80% and 90% (see Fig. 12), which in turn ensures that AFR increases with the increasing value of utilization (see Fig. 7).

Fig. 17 reveals the annual failure rates (AFR) of MAID-1 and MAID-2 with and without using the proposed disk-swapping strategy. The results plotted in Fig. 17 shows that for both MAID-1 and MAID-2, the disk-swapping process reduces the reliability of data disks in the disk system. We attribute the reliability degradation to the following reasons. MAID-1 and MAID-2 only store replicas of popular data; the reliability of the entire disk system is not affected by failures of cache disks. The disk-swapping processes increase the average utilization of data disks, thereby increasing the AFR values of data disks. Nevertheless, the disk-swapping strategy has its unique advantage. It is intended to reduce hardware maintenance cost by increasing the lifetime of cache disks.

Figure 18: Utilization Comparison of the MAID with MTTF and MTTDL
Access Rate Impacts on Utilization

We also observed from Fig. 17 that for the MAID-based disk system with the diskswapping strategy, a small threshold leads to a low AFR. Compared with the other two thresholds, the 2 ∗ 105 threshold results in the lower AFR. The reason is that when the access rate is 2 ∗ 105 No./month, the disk utilization is around 35% (see Fig.12), which lies in the monotone decreasing area of the curve shown in Fig. 7. Thus, disk swapping reduces AFR for a while until the disk utilization reaches 60%.

Fig. 18 shows the relationship between the access rate and utilization rate of MAID-1 and MAID-2 according to mean-time-to-data-lose (MTTDL) and the mean-time-to-failure (MTTF). Compared with the MTTDL, MTTF is more sensitive to the file access rate. The main reason is that the access rate impaction on the cache disks’ utilization will be took into account when using the idea of MTTF. However, even the cache disks are considered in MTTF, the utilization of the system doesn’t increase as sharply as what PDC does as shown in Fig. 10. Unlike PDC’s dealing with both data migrated in and out, the cache disks in MAID only deal with the data copied in which leads a lower utilization when the files access rate increased.

Fig. 19 reveals the AFR ofMAID-1 andMIAD-2 using the propsed disk-swapping strategy with the idea of the MTTDL and the MTTF. We notice that the AFRs of both MAID-1 and

MAID-2 with MTTF stay lower than that with MTTDL when the file access rate is lower than 5 ∗ 105. The main reason is that, after considering the utilization of the cache disks, the utilization of the whole system is pushed to 40% to 60%(shown in Fig. 18) which is the monotone decreasing part of the curve appeals in the Fig. 3. When the file access rate keeps increasing from 5 ∗ 105 to 10 ∗ 105, the AFRs with MTTF increase faster and stay higher than that with MTTDL because of the high utilization the system is when the cache disks are took into account.

Fig. 20 compares the AFR of the MAID-1 according to the MTTDL and the MTTF at different swapping threshold to the control group without disk swapping. And Fig. 21 reveals the AFR comparison of MAID-2 with MTTDL and MTTF. From the figures, we can see that when the file access rate is lower than 5 ∗ 105, the system with no swapping and using the idea of the MTTF has the lower AFR compare to others. Meanwhile, the system with swapping and using the idea of the MTTDL has the higher AFR. The reason is that the utilization of the system with MTTF decreases from 40% down to the trough of the curve shown in Fig. 3, which leads to the lower AFR. And at the same time, the utilization of the system with MTTDL lies around 30% which has a higher AFR.

When the file access rate is higher than 5 ∗ 105, the system without swapping and using MTTDL starts to keep the lowest AFR compare to others because of the ignoring of the cache disks which have increasing utilization that lead to the growth of the AFR. At the same time, the system without swapping and using MTTF has the highest AFR due to the noticeable amount of time that the cache disks spend on copying data from the data disks.

Since the PDC doesn’t have any of the data replica, any lose of the data leads to the failure of the system. In this case, the AFR results of PDC with both MTTDL and MTTF keep the same. Fig. 22 shows the AFR values of the parallel disk system where the PDCSwap1 and PDC-Swap2 strategies are employed. For comparison purpose, we also examined AFRs of the same disk without using any disk-swapping strategy. The results plotted in Fig. 22 indicates that the PDC-Swap1 and PDC-Swap2 strategies noticeably improve the reliability of the PDC-based parallel disk system by reducing the annual failure rate of the system. After comparing the three PDC-based disk systems, we observed that disk swapping reduces AFRs by nearly 5%. Compared with PDC-Swap1 strategy, PDC-Swap2 improves the reliability of the PDC-based system in a more efficient way. PDC-Swap2 is better than PDC-Swap1 because of the following reasons. First, PDC-Swap1 simply switches the most popular disks with the least popular disks whereas PDC-Swap2 swaps the most popular disks with the ones that have the least AFR values. Second, low utilization does not necessarily lead to a low AFR value due to the U-shaped curve appeared in Fig. 7. Third, the least popular disks may not be the ones with the lowest AFR value, meaning that PDC-Swap1 can not guarantee that the popular disks are always swapped with the disks with the lowest AFRs.

After comparing the results presented in Figs. 22, we observe that the improvement in reliability is sensitive to the threshold. More specifically, an increased threshold can give rise to the increase in the reliability improvement. This phenomenon can be explained as follows. After the disk swapping process, the utilization of the most popular disk is reduced down to the one with the lowest AFR of the entire parallel disk system. A higher threshold implies a larger utilization discrepancy between the pair of swapped disks. Importantly, regardless of the threshold value, AFR of the disk system continues increasing at a slow pace with the increasing value of access rate. This trend indicates that after each disk swapping, the utilizations of those disks with low AFRs are likely to be kept at a high level, which in turn leads to an increasing AFR of the entire disk system.

2.6 Conclusions[ Back to Top ]

In recognition that existing disk reliability models cannot be used to evaluate reliability of energy-efficient disk systems, we propose a new model called MINT to evaluate the reliability of a disk array equipped with reliability-affecting energy conservation techniques. We first model the impacts of disk utilization and power-state transition frequency on reliability of each disk in a disk array. We then derive the reliability of an individual disk from its utilization, age, temperature, and power-state transition frequency. Finally, we use MINT to study the reliability of disk arrays coupled with the MAID (Massive Array of Idle Disks) technique and the PDC (Popular Disk Concentration technique) technique. Compared our reliability model with other existing models, MINT has the following advantages:

• MINT captures the behaviors of PDC and MAID in terms of data movement/migration and power-state transitions.
• MINT seamlessly integrates multiple reliability-affecting factors into a coherent form.
• MINT can be used to evaluate the system-level reliability of a disk array.