CHEN-7250 Homework

Assignment No. 1

Due:  01/22, Fri

1. A tank contains water solution of A. The initial concentration of A in the tank is 10 g/L. At time = 0, additional A is fed into the tank at the rate of 1 L/minute. The concentration of A in the input stream is 20 g/L. At the same time the liquid in the tank is withdrawn through a pipe connected at the bottom of the tank. The flow rate through this pipe is v = (0.005)V, L/minute, where V is the volume of liquid in the tank. The liquid is well agitated. The density of liquid stays constant. A chemical reaction of A→B takes place in the tank:  r_A = - (0.08) C_A  g/L.min.

a. Using Polymath, determine the amount of A, the concentration of A, and volume of liquid in the tank when time = 50 minutes.

b. Repeat part (a) by hand calculation. Hint: Take N_A (not C_A ) as the dependent variable.

c. Calculate the conversion (X) in this reactor (considering the meaning of conversion) by Polymath when time = 50.

d. If this reactor is operated for a long period of time, it will eventually reach a steady-state turning into a CSTR. Calculate the conversion for this CSTR,

(i) By hand calculation using mole balance equation

(ii) By Polymath (taking a large number of t)

Assignment No. 2

Due: 01/27, Wed

Problem 3-17 

Additional Question: (c) Calculate the reaction time to achieve 50% conversion. Use polymath. Change k₁ value to 1000.

Assignment No. 3

Due: 01/29, Fri

1. Starting from mole balance equation of PFR, derive Eq. 4-17, p.170 for a second order isothermal gas reaction. Show the derivation process. Picking up the equation from the Appendix in not acceptable.

2. Problem 4-12 (a)

Assignment No. 4

Due: 02/01, Mon

1. Problem 4-7 (a), (b), (f) with a revision: redo (a) and (b) only.

2. Problem 4-13

Assignment No. 5

Due: 02/03, Wed

1. Problem 4-7 (e) and (f)-batch reactor. Ignore cost. Assume down-time for batch cycle (empting, cleaning, refill, etc.) = 4.5 hours.

2.

Hint: Prove in terms of Damkohler number.

Assignment No. 6

Due: 02/05, Fri

1. Problem 4-23 (a), (c).

Notes:

Set t(f) = 15,000.

Part (a): Conversion is based on ethylene chlorohydrin. Note unit of k is in hour, not minute.

Part (c): Consider using if( ) then( ) else( ) statement in Polymath. See Polymath examples

2. (Unsteady-State CSTR)

An elementary gas reaction, A —> 2B, is taking place in an unsteady-state CSTR. The reactor is initially filled with an inert gas. At time zero feed containing A only is fed into the reactor.

(a) Plot C_A, C_B, and C_I as a function of time

(b) How long would it take for C_B to reach 50% of C_A0?

(c) Calculate the conversion at this point and the steady-state conversion.

Additional information:

-rA = 0.1 CA mols A/(min,)(L)

Pressure is uniform at 1 atm throughout, T = 300°K, vo = 1 L/min., V = 40 L

Notes: Consider using total mole balance

and that N_T = N_A + N_B + N_I = constant in the reactor (IG Law).

Assignment No. 7

Due: 02/08, Mon

Problem 4-17 (a), (b)

Note: This is a trial and error problem with two unknown parameters (α and kC_A0²/F_AO).

Assignment No. 8

Due: 02/10, Wed

The following elementary liquid reactions are carried out by two different methods as described below. Using Polymath calculate the yield and the selectivity (S_DU) for each case.

A+B→D, k₁ = 0.25 (mol/L)^-1(minute)^-1

A+2B→U, k_2A = 0.66 (mol/L)^-2(minute)^-1

(Method 1)

Reactants A and B are kept in two separate vessels (Tank A and Tank B). The volume of each reactant is 50 liters. The concentration of reactant A is 0.8 mol/L and that of reactant B is 1.2 mol/L. The reactant B is poured abruptly into Tank A, mixed well, and the reaction is carried out in batch mode for 60 minutes.

(Method 2)

Reactant B is gradually added into Tank A at a constant flow rate of v₀ until Tank B is emptied (semi-batch operation). Assume the reaction stops at this point. The flow rate, v₀, is adjusted such that the final conversion of A is equal to that of Method 1. Note that t(f) varies depending on v₀.

Assignment No. 9

Due: 02/12, Fri

1. For an elementary reaction of A→ B→ C,

(a) Determine C_B and t_max (for C_B) in a batch reactor.

(b) Determine C_A, C_B, Cc, Y_B, and S_BC in a CSTR as function of t and k_i.

2. Problem 6-10 (a), (b), (c)

Additional question in part (b): Make plots of C_B, Y_B, S_BC, and conversion vs. temperature. Note that one can make a plot of any given function using Polymath by putting in a dummy differential equation in the DE section and list a given function in the EE (explicit equation) section.

Assignment No. 10

Due: 02/19, Fri

1. The following parallel reactions are taking place in a batch reactor for the duration of 30 minutes.

1

A → B

2

A → C

Data:

C_A0 =1.5 mol/L

k₁ = 0.012, k₂ = 0.002 min^-1 at 300^oK

E₁ = 6000 cal/mol, E₂ = 11000 cal/mol

(a) The reactor runs isothermally. Find the reaction temperature that will maximize production of B (C_B).

(b) The reactor is now to be operated non-isothermally. We will consider applying a temperature profile that changes linearly with time such that T = a + bt, where a and b are constants and t is reaction time. Find a and b that will maximize the production of B. Explain the difference in answers between part (a) and (b).

2. Problem 6-14 (a), (b), (c) (20-points)

Assignment No. 11

Due: 02/22, Mon

Problem 8-6 (a) – (d)

Assignment No. 12

Due: 02/24, Wed

1. Problem 8-9 (a) – (d) with the following revisions.

Change Ua/ρ_b to 3.0 (from 0.08) in (a)

Change α value to 0.0075 in (a-3)

Repeat (a-1) only in (b) and (d)

2. Problem 8-18

Ignore all the questions of (a)-(j).

Calculate the reactor temperature and conversion. There are more than one solutions. List all the solutions you can find.

Assignment No. 13

Due: 02/26, Fri

Problem 8-12 (a) – (d)

Assignment No. 14

Due: 03/04, Fri

Problem 8-18 (a)-(d), (f), (g)

Question (b) modified: What are the ignition, and extinction temperatures?

Assignment No. 15

Due: 03/09, Wed

1. The following liquid parallel reaction takes place in a PFR.

A → B, k₁ = 3.2x10^-4 (minute)^-1 at 300^°K

A → C, k₂ = 1.2x10^-5 (minute)^-1 at 300^°K

E₁ = 18,000 cal/mol

E₂ = 24,000 cal/mol

v_o = 2.0 L/min

V= 10L

C_AO = 1.0 mol/L

C_pA = C_pB = C_pc =18.0 cal/mol

Cp coolant = 1 cal/g

H_A = 5,000 cal/mol

H_B = 1,600 cal/mol

H_C = 4,000 cal/mol

Ua = 4.0 cal/min.^°K.L

To = Feed temperature = 350^°K

Tao = Inlet coolant temperature =310^°K

(a) The PFR is a shell-and-tube type with co-current cooling. Determine the flow rate of coolant (mc, g/minute) that will maximize production of B. Calculate the yield of B and Selectivity (B/C) and conversion of A under this condition.

(b) Determine the mc_opt for maximum production of B under the constraint that

Y_B/A > 0.8

2. (20-points max.)

The following multiple gas reaction takes place in a CSTR.

1 2

A →B →C

3↓

2D

Data:

The reaction is elementary.

Feed: Pure A, P_AO = 4 atm, vo = 5 L/minute, To = 300^°K Reactor volume = 100 L

k₁ = 1.5x10^-2, k₂ = 8.9x10^-4, k_3B = 2.5x10^-4 minute^-1 at 300^°K

E₁ = 5600, E₂ = 6000, E₃ = 7000 cal/mol

(a) Find the optimum reactor temperature that will maximize production of B.

(b) Repeat (a ) with a constraint that SCD >1.5

(c) We now have the following additional information.

C_PA = C_PB = C_PC = 16.0 cal/mol.^°K

C_PD = 10.0 cal/mol.^°K

H_A^° = 14600 cal mol, H_B^° = 5500 cal mol, at 298^°K

Hc^° = 4000 cal mol, H_D^° = 3000 cal mol, at 298^°K

Note that ∆Cp ≠ 0 for reaction No.3.

The reactor runs at 400^°K.

Calculate Q (heating or cooling rate).

Assignment No. 16

Due: 03/11, Fri

Problem 9-5 with the following revision.

k_r = 0.002 min^-1

Assignment No. 17

Due: 3/21, Mon

Problem 5-6. (a), (b). Use differential and integral linear methods in (a).

Assignment No. 18

Due: 03/23, Wed

1. Problem 5-9.

Try both differential linear and integral linear methods in part (a).

2. Problem in CD: P5-G_B.  

The oxidation of propene (P) to acrolein (A) was carried out over a Mo-Pr-Bi catalyst [Ind. Eng. Chem. Res., 26, 1419 (1987)].

CH₃CH=CH₂+O₂CH₂=CHCHO+H₂O

It has been proposed to correlate the data using the power law model

for the rate law [cf. Equation (5-2)].

r_acrolin = k P_p^αP₀₂^β

The reaction was carried out in a differential reactor with 0.5 g of catalyst at 623 K. From the data below, determine the reaction orders with respect to propene, α, and oxygen, β, and the specific reaction rate, k.

where

F_A=exiting molar flow rate of acrolein, mmol/h
P_P= entering partial pressure of propene, atm
P_O2= entering partial pressure of oxygen, atm

Solve by differential linear and nonlinear method.

Assignment No. 19

Due: 03/25, Fri

Problem 7-11 (a), (b). Consult Eq. 7-26

Assignment No. 20

Due: 03/28, Mon

Problem 5-5 (a), (b).

Assignment No. 21

Due: 04/04, Mon

1. Show that

where and L = half the slab thickness

2. Problem 12-6 (a), (b)

Assignment No. 22

Due: 04/06, Wed

1. Using Polymath, calculate the effectiveness factor for a flat-plate catalyst carrying out a second-order reaction,

where, = 3.0

2. Derive a differential equation describing C_A vs. r in a long cylindrical catalyst, wherein a first-order reaction is taking place.

a. Put the DE and the boundary conditions into dimensionless form.

b. Calculate the effectiveness factor using Polymath and by the analytical solution (Bessel function solution), where = 8.0

c. Estimate an approximate effectiveness factor using the flat-plate solution and appropriate value (a universal Thiele modulus).

Assignment No. 23

Due: 04/08, Fri

A catalytic reaction experiment was carried out using a differential reactor packed with spherical catalyst particles. The catalysts were then taken out of the reactor, cut into two pieces (hemi-sphere form), reloaded, and the same experiment was repeated. The data indicate the reaction rate increased by 20% in the second experiment. Estimate the effectiveness factor and the Thiele modulus for the spherical catalyst. Assume first-order reaction.

Assignment No. 24

Due: 04/09, Mon

1. (5 points): From the class notes of April 8 (the last Equation of Bischoff analysis) prove that

∅g = 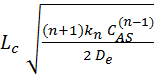for n^th order reaction.

-r_A= k_n C_ASⁿ, ∅_g = generalized Thiele modulus for nth order reaction

2. A catalytic elementary gas reaction of 2A → B +C was investigated for diffusion effect using a differential flow reactor under the following conditions.

Amount of catalyst = 50 grams

Spherical catalyst with 0.6 cm diameter

Density of catalyst = 1.6 grams/cm³

De = 1.2x10^-4 cm²/sec

Feed: Pure A, P=3 atm, T=350^°K, v_o = 14 cm³/sec,

The concentration of B (C_B) coming out of the differential reactor was measured to be 3.75x10^-6 mols/cm³.

(a) Calculate (-r_A)_obs based on the catalyst volume.

(b) Using one-point method, estimate the effectiveness factor and the rate constant.

Above information is to be used to design a PBR to carry out the following reaction. Feed conditions are the same as above. Reactor is isothermal.

Additional information: F_AO = 72 mols/hour

Required conversion = 0.9

α = 1.65x10^-5 g^-1

(c) Calculate the required amount of catalyst. Plot conversion, y, and η vs. V_catalyst.

Pay attention to the units in concentration and time: cm³ vs. L, hour vs. s.

Assignment No. 25

Due: 04/15, Fri

Problem 12-16 (a), (b)

Notes: Keep units consistent: all volume units in cm³, time units in seconds. Use linear regression.

The reactor in this problem is a catalytic CSTR with W = 160 g.

Assignment No. 26

Due: 04/20, Wed

Derive the RTD function for two CSTRs connected in series:

V₁ = 10 liters, V₂ = 20 liters, v₀ = 10 liters/ minute.

Make a plot of the RTD.

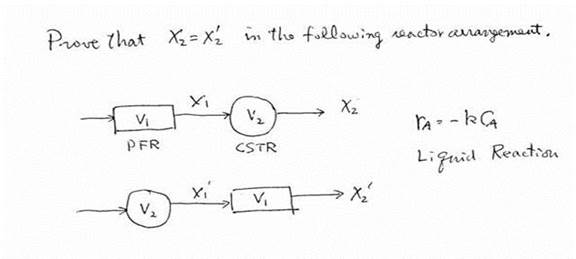
Prove that .

Assignment No. 27

Due: 04/22, Fri

Using Polymath, plot RTD function, and calculate τ and σ_ϴ² for Assignment 26. Repeat for V₁ = V₂ = 15.

Assignment No. 28

Due: 04/25, Mon

1. From a tracer test of a continuous reactor, the following data are obtained.

ti	0	1	2	3	4	5	6	8	10	12
Ci	0	1.2	4.0	3.5	3.0	2.6	2.0	1.0	0.4	0.0

(a) Using Excel, estimate τ, s_q², and conversion.

Additional data:

2^nd order reaction, k = 0.6 L/mol.minute, C_A0 = 1.0 mol/L.

(b) Compare the conversion with those of PFR and CSTR.

2. Problem 13-19, (a)-(h), (m), (o), (p). (20 points)

Use Polymath.

Assignment No. 29

Due: 04/27, Wed

Problem 14-13, (d)-(g) (20 points)

Additional notes:

For the sake of uniform answer, take σ² = 75.4 and τ = 9.93 from the previous HW 13-19.

Note that τ₁ = τ₂ = τ/2

(d): Ignore open system. Solve by polymath and also by Eq. 14-27, p971

(g): Solve by mole balance using Polymath.