1. Quick Python Programming with Semiconductor Device Fundamentals¶
1.1. Objectives¶
- Getting you up and running with python programming fundamentals
- Make 2D plots such as band diagrams
1.2. Motivation¶
I have been asked by several past students that took my semiconductor Elec6700, 7710 and 8710 courses to offer a python class, which I have not been able to do. I created tutorials in Onenote in the past and spent 2-3 lectures on python.
This is a new one specifically written for Elec6710 class 2013 students that are new to programming or new to python.
We will use a relatively simple room temperature equilibrium semiconductor problem which is at the center of our first chapter on fundamentals. Complete ionization of dopants is assumed so that analytical solution can be used. Elec2210 students can also use this except for the band diagram drawing part.
My purpose is to give you a real example so you can learn from the process of solving this problem.
You should type codes yourself in front of a computer, and then modify it step by step - instead of copy and paste. You miss a lot of learning opportunities that way.
1.3. Required Programs¶
- EPD Python, now called Canopy. Request academic license so you have more libraries to use as is.
- myplot.py from our on-line folder
1.4. Install EPD python Canopy and Getting myplot.py¶
Visit https://www.enthought.com/products/canopy/academic/ and request an academic license. Click the “Request your Academic License” button, and follow instructions.
Using your academic email address, you will need to register for a free EPD account, or log in to your existing EPD account. They provide windows, Mac and Linux versions. I use and recommend 64 bit.
1.4.1. Launch Canopy¶
Find Canopy from your program list and run it. In windows 8, press Windows key, then type “canopy” and select it from search result.
1.4.2. Create a source file¶
File->New Editor Window. You can create a new file in a working directory of your choice.
File->Save as. Pick a file name indicating what the program does, e.g. eqsemiv0.py, create a new folder or place it in an existing folder.
1.4.3. Getting the myplot.py¶
First let us make sure we have the “myplot.py” file in the same directory as your eqsemiv0.py. This has a function I wrote to ease 2d plotting of data.
Numbers are good, but plots are much more powerful. I want to make your life easier and jump start it for you. If not, copy and paste it in there. Verify it in explorer.
Filename should NOT be changed.
1.5. Example of Equilibrium Semiconductor Problem¶
Let us look at our technical problem description first, and then translate this into computational thoughts which we can use for programming.
1.5.1. Problem Statement¶
Given effective density of states Nc, Nv, bandgap Eg values at t=300K, write a program that calculates p, n and all band energies Ec, Ev, Ef, Ei for a given donor concentration Nd and acceptor concentration Na, solve for hole and electron concentrations p and n first using the solution given below. Generate plots showing how p, n and the energy band levels vary with Nd and Na.
Intrinsic carrier concentration:
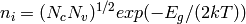
If Nd > Na:
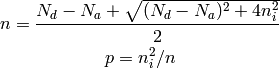
If Na > Nd:
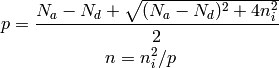
1.5.2. Problem analysis¶
After reading this, we realize
We need Boltzmann constant
We have all the equations.
We need the math functions like exp, sqrt, taking power, e.g. ni^2.
We can write a function for finding p and n from a given Nd and Na. An inspection of the equations show that we also need ni, which can be calculated first from Nc, Nv, Eg, T.
We can try to write a function, say we call it find_pn(nd, na, ni). We can then call this function repeatedly in a loop when we need to vary Nd or Na.
We also need to have a range of Nd or Na to make plots. It is not given to us, so we have some flexibility. Let us say from 1e5 to 1e20.
In general it is good practice to separate codes for calculating data and codes for plotting data. Divide and conquer of course applies in general.
1.5.3. Interactive Python Shell for Quick Experiments/Quick Start¶
An excellent starting place is the interactive shell located at the bottom of your Editor-Canopy window. Often in writing python codes, you forget about certain things, or are not so sure what the result of “1/2” is, you can quickly figure this out by typing on the command line of a “python interpreter” or “python shell”.
Welcome to Canopy's interactive data-analysis environment!
with pylab-backend set to: qt
Type '?' for more information.
In [1]: 1/2
Out[1]: 0
That is because in python, integer/another integer is still an integer.
Most of the time, this is not what we want. We can get around by:
In [2]: 1/2.0
Out[2]: 0.5
Or I will suggest that we rewrite how “/” operator works. Well that has been done, so let us just import the codes that does that instead of reinventing the wheel.
In [3]: from __future__ import division
In [4]: 1/2
Out[4]: 0.5
__future__ is a module, understand it as a collection of functions for now, we just import the “division” function which will change how “division” operator works. A module is just a collection of functions (in the broad sense).
Let us also test out the “taking power” operator, which is ** in python.
In [8]: ni=1e10
In [9]: ni**2
Out[9]: 1e+20
Where do I find all this information? Pick up any online python tutorial, or the official documentation at http://docs.python.org/2/ where you will find the language reference: http://docs.python.org/2/reference/index.html. Or simply google it.
1.5.4. A Python Jump Start with ni¶
Let us now create or open the file “equisemiv0.py” in our working directory, e.g. a “elec6710” directory under your home directory. Make sure the “myplot.py” file exists in that directory too.
Type in the following codes for ni calculation:
# use newer python3 print and 1/2=0.5
from __future__ import division, print_function
from math import exp, sqrt, log
# Boltzmann constant
KB = 8.6173e-5 #eV/K
# Using 300K parameters
t = 300 # K
nc = 2.8e19 #/cm^3
nv = 1.04e19 #/cm^3
eg = 1.124 #eV
# calculate kt and ni
kt = KB*t # eV
nisquare = nc*nv*exp(-eg/kt)
ni = sqrt(nisquare)
print(ni)
print(ni/1e10)
The first line is just comments. Anything after the hash character, # are comments. Comments are used to clarify code and are not interpreted by Python. For instance, we use #eV/K to indicate the Boltzmann constant unit is eV/K.
from __future__ import division, print_function simply imports the newer division and print function from the __future__ module. A module is a collection of library functions.
from math import exp, sqrt, log imports several math functions from the math module, with intuitive names like found in any other language.
A few variables KB, nc, nv, eg are then created through assignment =. Values, in this case, numbers are assigned to variables.
The + - * / operators work just like you expect. The print() function is called to print ni. We also normalize it to 1e10 so that we do not have to deal with formatting numbers for printing, just for now.
Then click the Green Run button or use Ctrl+R to run your program. In the python shell, you will find output:
In [10]: %run C:/Users/G/pythonsemi3/py6710/eqsemiv0.py
6178382274.3
0.61783822743
We see the ni value obtained is on the correct order of 1e10, which tells us we are probably correct in everything so far.
Now add these two lines of codes to the end and rerun it:
text = "intrinsic concentration is: {ni:5.2e} /cm^3".format(**locals())
print(text)
The output is:
In [11]: %run C:/Users/G/pythonsemi3/py6710/eqsemiv0.py
6178382274.3
0.61783822743
intrinsic concentration is: 6.18e+09 /cm^3
text is assigned a string. Double quotes or single quotes can be used to create string. {ni:5.2e} tells python it is going to insert ni here, with exponential format, width is 5, and number of digital after decimal point is 2. .format() is a method or function of the string "intrinsic concentration is: {ni:5.2e} /cm^3". How does the string get the value of ni? It cannot get it from the current ni value automatically. Instead, we need to pass the value of ni to it.
The easiest way to do this is to just use **locals() as argument of the .format() method. This is an advanced feature, so I will not go any deeper. Just do this for now and generation of text for output or graph labels from variables will be straightforward.
1.5.5. Function for finding p and n¶
Since we are asked to repeat p and n calculations for many different Nd or Na, it makes sense to put this task into a function.
An inspection of the p and n equations show that Nd, Na and ni values are inputs, while p and n are outputs.
Type the following codes at the end of the same python file for the find_pn() function.
# define a function for finding p and n from given nd, na, and ni
def find_pn(nd=0, na=0, ni=1e10):
# indent - body of function
# this is a doc string - kind of like comments, but a string
'''
for given nd, na, solve
mass action law and neutrality equations to determine n and p
at equilibrium condition.
'''
# calculate net doping ndop
ndop = nd - na
# ni^2
ni2 = ni**2 # note how to calculate power using **
ndop2 = ndop**2
# to avoid numerical problem, treat ndop >0 and <0 separately
# see our notes for equation/derivation
if ndop > 0:
tmp = ndop + sqrt(ndop2 + 4 * ni2)
n = tmp / 2.0
p = ni2 / n
else:
ndop = -1 * ndop
tmp = ndop + sqrt(ndop2 + 4 * ni2)
p = tmp / 2.0
n = ni2 / p
# return results in a dictionary
# the order of items is not important
return dict(nd=nd,
na=na,
p=p,
n=n,
ni=ni)
Save your code. We have introduced several new features.
def starts a function definition. It must be followed by the function name, here find_pn(), and the parenthesized list of formal parameters, nd, na, ni. Default values are given, in case they are not provided by function caller. The def statement ends with a colon :.
The body of the function must be indented. This is how python identifies code blocks, by indentation. Indent to begin a block, dedent to end a block. Statements that expect an indentation level end with a colon :.
The first statement is a string literal, which we could have left out. It is the function’s docstring, or documentation string, kind of like a help for users of the function.
The if and else statements are used to use different equations depending on Nd>Na or Na>Nd. Again, code blocks are defined by indentation next to the :.
The return statement returns result. In other languages, you would do something like return p, n, nd, na, ni which works just fine in python. However, you will have to remember clearly the first in the list of function return is p, second is n, and so on. It quickly gets confusing and you can easily make a mistake. In addition, codes for processing function return are hard to write if you need to dynamically pick what you really need from a long list of returns.
Here we return a dictionary which is like a look-up table. The dictionary is created with the dict() function, and a list of key = value arguments. Run the code, then type in the python shell window at the bottom:
In [13]: pn = find_pn(nd=1e16, na=0, ni=ni)
In [14]: pn
Out[14]:
{'n': 1.0000000000003816e+16,
'na': 0,
'nd': 1e+16,
'ni': 6178382274.2980175,
'p': 3817.240752734538}
In [15]:
pn is assigned result of the find_pn() function, which is a dictionary. If we want to access n and p:
In [19]: pn['p']
Out[19]: 3817.240752734538
In [20]: pn['p']*pn['n']
Out[20]: 3.817240752735995e+19
In [21]: ni**2
Out[21]: 3.817240752735995e+19
In [22]:
1.5.6. Iteration over an array of Nd¶
Now let us iterate over an array of Nd. Let us add more codes:
# make a plot of p/n versus nd
from numpy import logspace, empty
from myplot import myplot, show, new_ax
# create an array of nd, on log scale, from 1e5 to 1e20
nds = logspace(5, 20, 5)
# create place holders for p and n arrays
ps = empty(len(nds))
ns = empty(len(nds))
# iterate over array nds, we also need index, so use "enumerate"
for idx, nd in enumerate(nds):
# !!! Note indentation is used here to define body of the for loop
solution = find_pn(nd=nd, na=0, ni=ni)
# see how we get p and n by key (name) in dictionary
ps[idx] = solution['p']
ns[idx] = solution['n']
Run. In the python shell, type:
In [23]: nds
Out[23]:
array([ 1.00000000e+05, 5.62341325e+08, 3.16227766e+12,
1.77827941e+16, 1.00000000e+20])
In [24]: ps
Out[24]:
array([ 6.17833227e+09, 5.90360617e+09, 1.20711291e+07,
2.14659222e+03, 3.81724075e-01])
In [25]: ns
Out[25]:
array([ 6.17843227e+09, 6.46594750e+09, 3.16228973e+12,
1.77827941e+16, 1.00000000e+20])
In [26]:
logspace() is used to generate an array ranging from 1e5 to 1e20, with 5 points for illustration convenience. You will normally use 50 points or more for smooth curves. empty() is used to create place holders for p and n arrays.
for idx, nd in enumerate(nds):
# !!! Note indentation is used here to define body of the for loop
solution = find_pn(nd=nd, na=0, ni=ni)
# see how we get p and n by key (name) in dictionary
ps[idx] = solution['p']
ns[idx] = solution['n']
creates a for loop over elements of the nds array. idx is an index, and nd a value generated by enumerate(). idx is needed to address elements of ps and ns. The square brackets are used to access array elements, just like they were used to access dictionary elements. Recall find_pn() returns a dictionary that contains p and n.
1.5.7. Visualize data with plots¶
Let us go back and change the number of Nd points to 50. See if you can do this yourself:
# create an array of nd, on log scale, from 1e5 to 1e20
nds = logspace(5, 20, 50)
Save. Go to end of your file, add:
# Must dedent now to get out of the body of the for loop
# create an empty figure / ax for plotting
ax = new_ax()
# plot ns versus nds, log scale for both x and y
# color, label for legend
# xlabel and ylabel for x- and y-axis
linep, axpn, fig = myplot(ax=ax,
x=nds,
y=ns,
xlog=True,
ylog=True,
color='r',
label='n',
xlabel='$N_d (/cm^3)$',
ylabel='$p,n(/cm^3)$')
# continue to plot p on the same ax
linen, axpn, fig = myplot(ax=ax, x=nds, y=ps, color='b',
label='p')
# save figure to a PDF
# fig is an object, and has a method savefig
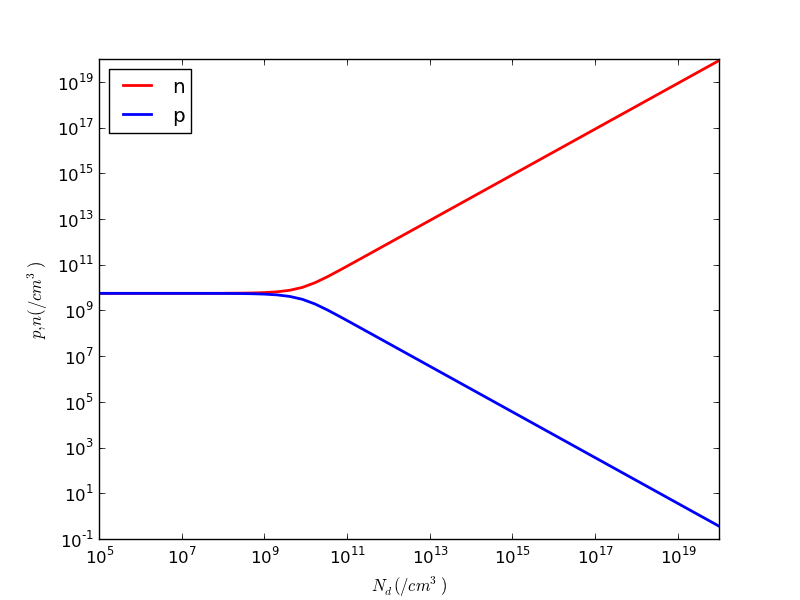
fig.savefig('pnvsnd.pdf')
A plot is a bunch of points on a pair of x- and y-axis. Here
ax = new_ax()
creates a pair of axes. We then use my myplot() function to plot ns versus nds, using log scale for the x-axis as well as y-axis, in red color, with a label for use in legend, and proper x- and y-axis labels, all in just one statement. The xlabel and ylabels use Latex style syntax for formatting text.
The myplot() function call returns the curve or line, the axis, and the figure that contains the axis. We could have multiple axes or subplots in one figure.
As we desire to overlay p and n, we simply pass the same ax to the ax parameter.
fig has a method savefig() which we use to save the figure as a PDF file.
Run. Browse your folder, and you should find the PDF file. If not, type in the python shell to find out your path of working directory:
In [35]: ls *.pdf
Volume in drive C is Windows
Volume Serial Number is 9C65-4616
Directory of C:\Users\G
09/02/2013 02:39 PM 17,088 pnvsnd.pdf
1 File(s) 17,088 bytes
0 Dir(s) 57,659,203,584 bytes free
In [36]: ls *.png
Volume in drive C is Windows
Volume Serial Number is 9C65-4616
Directory of C:\Users\G
09/02/2013 02:45 PM 32,119 pnvsnd.png
1 File(s) 32,119 bytes
0 Dir(s) 57,659,207,680 bytes free
In [37]:
Here is the pnvsnd.pdf I generated.
Well, where is the figure on screen? To actually show the plot on screen, we call the “show” function imported earlier. Just add to the end of your code:
show()
Run. You should see a graph popping up.
1.5.8. Find band energies¶
Remove the last line with show(). Add these codes to the end:
# now let us write a function to calculate ni and kt
def find_ni_kt(nc=2.8e19, nv=1.04e19, eg=1.124, t=300):
# calculate kt and ni
kt = KB*t # eV
nisquare = nc*nv*exp(-eg/kt)
ni = sqrt(nisquare)
return dict(ni=ni, kt=kt)
def find_energies(nd=1e16, na=0, eg=1.124, nc=2.8e19, nv=1.04e19, t=300):
'''
find energies using ev as 0, or reference.
'''
ni_kt = find_ni_kt(nc=nc, nv=nv, eg=eg, t=t)
ni = ni_kt['ni']
kt = ni_kt['kt']
ev = 0
ec = ev + eg
ei = (ec+ev)/2 + kt/2 * log(nv/nc)
solution = find_pn(nd=nd, na=na, ni=ni)
n = solution['n']
ec_minus_ef = kt*log(nc/n)
ef = ec - ec_minus_ef
return dict(ev=ev,
ec=ec,
ei=ei,
ef=ef)
solution = find_energies(nd=1e16, na=0, eg=eg, nc=nc, nv=nv, t=t)
keys = solution.keys()
bands = dict()
num_nds = len(nds)
for key in keys:
bands[key] = empty(num_nds)
for idx, nd in enumerate(nds):
solution = find_energies(nd=nd, na=0, eg=eg, nc=nc, nv=nv, t=t)
for key in keys:
bands[key][idx] = solution[key]
# now data is ready, let us plot them out
from myplot import ColorCycler
cc = ColorCycler()
axbands = new_ax()
for key in keys:
myplot(ax=axbands,
x=nds,
y=bands[key],
xlog=True,
color=cc.next(),
label=key)
axbands.set_xlabel('$N_d(/cm^3)$')
axbands.set_ylabel('$Energies (eV)$')
# change bottom of y-axis so that ev=0 can be clearly seen
axbands.set_ylim(bottom=-0.2)
show()
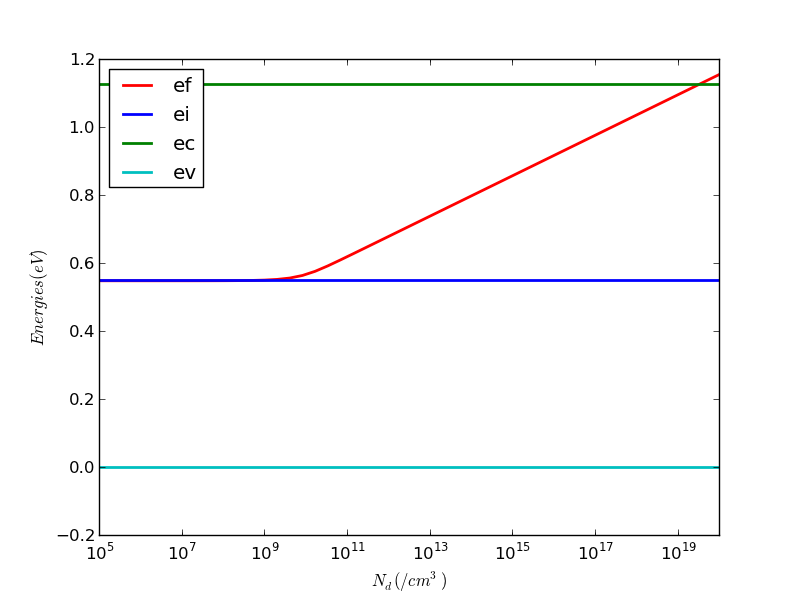
Run. You should see a nice band diagram showing how all the energies vary as you increase Nd. When Nd << ni, Ef is at Ei. Only when Nd >> ni, Ef increases with Nd. You will find a slope of 60meV increase per 10x or one decade increase of Nd when this happens.
You should be able to understand about 70% of this code section. We have defined two new functions, find_ni_kt() and find_energies().
The find_energies() function solves all the energies for a given set of parameters, and returns the energy solution as a dictionary. We can easily see this by typing solution in the python shell:
In [41]:
In [42]: solution
Out[42]: {'ec': 1.124, 'ef': 1.1569085813545472, 'ei': 0.5491981558716709, 'ev': 0}
In [43]: solution.keys()
Out[43]: ['ef', 'ei', 'ec', 'ev']
In [44]:
solution is a dictionary, and it has a method keys(), which returns a list of all the dictionary keys.
bands = dict()
num_nds = len(nds)
for key in keys:
bands[key] = empty(num_nds)
creates a bands dictionary, for each key, that is each of [‘ef’, ‘ei’, ‘ec’, ‘ev’], an empty array of the same size as nds is created.
for idx, nd in enumerate(nds):
solution = find_energies(nd=nd, na=0, eg=eg, nc=nc, nv=nv, t=t)
for key in keys:
bands[key][idx] = solution[key]
Here we iterate through all Nd values with index using the enumerate() function, an iterator actually as you build up more python understanding. For each nd, we get a energy solution dictionary solution. We take them out by iterating over all keys.
Since we already created an array for each key, that is, bands[key], we just need to assign the solution for each key, solution[key] to the corresponding array element bands[key][idx].
If you get lost, try this in the python shell:
In [44]: key = 'ec'
In [45]: bands[key]
Out[45]:
array([ 1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124,
1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124,
1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124,
1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124,
1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124,
1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124, 1.124,
1.124, 1.124])
In [46]: bands[key][0]
Out[46]: 1.1240000000000001
In [47]:
We could have done all of these by simply creating multiple arrays of band energies manually. The code will be less flexible. However, if you find this section of codes difficult for you to grasp, just do what you feel comfortable or follow your intuition and experiment with your own ideas.
1.5.9. Plot band diagrams versus doping¶
Hang in there, you have done a lot at this point. Now it is time to plot out the band energies, Ec, Ev, Ef, Ei versus Nd. We would like to use a different color for each curve. You can use my ColorCycler class to create an object, everything in python is an object.
Add this code to end of your file:
# now data is ready, let us plot them out
from myplot import ColorCycler
cc = ColorCycler()
axbands = new_ax()
for key in keys:
myplot(ax=axbands,
x=nds,
y=bands[key],
xlog=True,
color=cc.next(),
label=key)
axbands.set_xlabel('$N_d(/cm^3)$')
axbands.set_ylabel('$Energies (eV)$')
# change bottom of y-axis so that ev=0 can be clearly seen
axbands.set_ylim(bottom=-0.2)
show()
Run. You should see a nice band diagram with Nd as x-axis, in log scale. cc is a ColorCycler object, cc.next() cycles through all colors.
axbands also has methods like set_xlabel() and set_ylabel(). axbands.set_ylim(bottom=-0.2) changes the bottom of the y-axis to -0.2 so that ev=0 can be clearly seen.
Try commenting this line out to see the difference.
1.6. Make codes more pythonic and program template¶
Now we can better organize our codes to make it more pythonic.
For one, we have lots of global variables, they can cause problems as your program gets more complex and should be used sparely and wisely.
It is custom to organize a python program like this:
# this is a template made to illustrate the typical
# structure of a python program
# import functions here
from __future__ import division, print_function
from numpy import linspace, exp
from myplot import myplot, show
# some worthwhile global variables
# Boltzmann constant
KB = 8.6173e-5 #eV/K
# some functions
def find_ic(isat, vbe, t):
kt = KB * t
pt = kt
ic = isat * (exp(vbe/pt)-1)
return ic
def main():
t = 300
isat = 1e-15
vbe = linspace(0.1, 1.0, 50)
ic = find_ic(isat, vbe, t)
myplot(x=vbe, y=ic,
xlabel='$V_{BE} (V)$',
ylabel='$I_C (A)$',
label='$I_C$',
ylog=True,
color='b')
if __name__ == '__main__':
main()
show()
You start with imports, then some global variables for things like constants, then some helper functions, and ultimately a main() function.
The last if statement is True when you run the file, so main() is called. The show() call displays all graphics on screen if they have not been displayed. Python separates graphics calculation and display by default. The behavior can be changed if you run your program in the so-called interactive mode. If you are using Canopy, the default mode is interactive.
With this, try modifying our equilibrium p/n and bands plotting program to make it more pythonic. It will also make reuse of codes and future modification much easier. An example is:
# use newer python3 print and 1/2=0.5
from __future__ import division, print_function
from math import exp, sqrt, log
from numpy import logspace, empty
from myplot import myplot, show, new_ax
# These are "global" variables to this file
# I am not against use of global variables
# However, I do think they should be used sparely and wisely.
# You can run into some serious issues if you use lot of global variables
# Boltzmann constant
KB = 8.6173e-5 #eV/K
# Using 300K parameters so let us be clear that all parameters are for 300k
# t = 300 # K
nc300k = 2.8e19 #/cm^3
nv300k = 1.04e19 #/cm^3
eg300k = 1.124 #eV
# now let us write a function to calculate ni and kt
def find_ni_kt(nc=nc300k, nv=nv300k, eg=eg300k, t=300):
'''
returns ni and kt in a dictionary
Usage:
find_ni_kt(nc=2.8e19, nv=1.04e19, eg=1.124, t=300)
Example:
nikt300k = find_ni_kt()
ni300k = nikt300k['ni']
kt300k = nikt300k['kt']
'''
# calculate kt and ni
kt = KB*t # eV
nisquare = nc*nv*exp(-eg/kt)
ni = sqrt(nisquare)
return dict(ni=ni, kt=kt)
nikt300k = find_ni_kt()
# calculate ni300k and kt300k for convenience use
ni300k = nikt300k['ni']
kt300k = nikt300k['kt']
# define a function for finding p and n from given nd, na, and ni
def find_pn(nd=0, na=0, ni=ni300k):
# indent - body of function
# this is a doc string - kind of like comments, but a string
'''
for given nd, na, solve
mass action law and neutrality equations to determine n and p
at equilibrium condition.
'''
# calculate net doping ndop
ndop = nd - na
# ni^2
ni2 = ni**2 # note how to calculate power using **
ndop2 = ndop**2
# to avoid numerical problem, treat ndop >0 and <0 separately
# see our notes for equation/derivation
if ndop > 0:
tmp = ndop + sqrt(ndop2 + 4 * ni2)
n = tmp / 2.0
p = ni2 / n
else:
ndop = -1 * ndop
tmp = ndop + sqrt(ndop2 + 4 * ni2)
p = tmp / 2.0
n = ni2 / p
# return results in a dictionary
# the order of items is not important
return dict(nd=nd,
na=na,
p=p,
n=n,
ni=ni)
def plot_pn_vs_nd():
# make a plot of p/n versus nd
# create an array of nd, on log scale, from 1e5 to 1e20
nds = logspace(5, 20, 50)
# create place holders for p and n arrays
ps = empty(len(nds))
ns = empty(len(nds))
# iterate over array nds, we also need index, so use "enumerate"
for idx, nd in enumerate(nds):
# !!! Note indentation is used here to define body of the for loop
solution = find_pn(nd=nd, na=0, ni=ni300k)
# see how we get p and n by key (name) in dictionary
ps[idx] = solution['p']
ns[idx] = solution['n']
# Must dedent now to get out of the body of the for loop
# create an empty figure / ax for plotting
ax = new_ax()
# plot ns versus nds, log scale for both x and y
# color, label for legend
# xlabel and ylabel for x- and y-axis
linep, axpn, fig = myplot(ax=ax,
x=nds,
y=ns,
xlog=True,
ylog=True,
color='r',
label='n',
xlabel='$N_d (/cm^3)$',
ylabel='$p,n(/cm^3)$')
# continue to plot p on the same ax
linen, axpn, fig = myplot(ax=ax, x=nds, y=ps, color='b',
label='p')
# save figure to a PDF
# fig is an object, and has a method savefig
#fig.savefig('pnvsnd.pdf')
fig.savefig('pnvsnd.png')
def find_energies(nd=1e16, na=0, eg=eg300k, nc=nc300k, nv=nv300k, t=300):
'''
find energies using ev as 0, or reference.
'''
ni_kt = find_ni_kt(nc=nc, nv=nv, eg=eg, t=t)
ni = ni_kt['ni']
kt = ni_kt['kt']
ev = 0
ec = ev + eg
ei = (ec+ev)/2 + kt/2 * log(nv/nc)
solution = find_pn(nd=nd, na=na, ni=ni)
n = solution['n']
ec_minus_ef = kt*log(nc/n)
ef = ec - ec_minus_ef
return dict(ev=ev,
ec=ec,
ei=ei,
ef=ef)
def plot_bands_vs_nd():
solution = find_energies(nd=1e16, na=0, eg=eg300k, nc=nc300k, nv=nv300k, t=300)
keys = solution.keys()
bands = dict()
# create an array of nd, on log scale, from 1e5 to 1e20
nds = logspace(5, 20, 50)
num_nds = len(nds)
for key in keys:
bands[key] = empty(num_nds)
for idx, nd in enumerate(nds):
solution = find_energies(nd=nd, na=0, eg=eg300k, nc=nc300k, nv=nv300k, t=300)
for key in keys:
bands[key][idx] = solution[key]
# now data is ready, let us plot them out
from myplot import ColorCycler
cc = ColorCycler()
axbands = new_ax()
for key in keys:
myplot(ax=axbands,
x=nds,
y=bands[key],
xlog=True,
color=cc.next(),
label=key)
axbands.set_xlabel('$N_d(/cm^3)$')
axbands.set_ylabel('$Energies (eV)$')
# change bottom of y-axis so that ev=0 can be clearly seen
axbands.set_ylim(bottom=-0.2)
def main():
plot_pn_vs_nd()
plot_bands_vs_nd()
if __name__ == '__main__':
main()
show()
1.7. Adding T dependence¶
Now you can add temperature dependence. Below are several functions you may use for calculating Nc, Nv, and Eg as a function of T.
from __future__ import division
def eg_from_t(t):
eg = 1.17 - 4.73e-4*(t**2/(t+636))
return eg
def nc_from_t(t):
nc = 6.2e15*t**(3/2)
return nc
def nv_from_t(t):
nv = 3.5e15*t**(3/2)
return nv
1.8. Homework Exercises¶
Try writing a few function for each task below and call the functions from the main() function. You can use my example functions as a starting point. Only minor changes are required in all cases.
- Plot out p and n versus Nd, Nd range is from 1e14 to 1e20. You have a background Na of 1e16.
- Plot out bands Ec, Ev, Ef, Ei versus Nd, Nd range is from 1e14 to 1e20. You have a background Na of 1e16.
- Plot out p and n versus Na, Na range is from 1e14 to 1e20. You have a background Nd of 0.
- Plot out bands Ec, Ev, Ef, Ei versus Na, Na range is from 1e14 to 1e20. You have a background Nd of 0.
1.9. Other python resources¶
If you have had absolutely no programming experience at all, the beginner tutorials at http://wiki.python.org/moin/BeginnersGuide/NonProgrammers might be useful.
Amng those, you may start with A Byte of Python, which can be downloaded from http://www.swaroopch.org/notes/Python
I also wrote a tutorial with in-depth discussion of python objects and functions for Elec6700. That is posted at http://www.eng.auburn.edu/~niuguof/_downloads/py.pdf